题目内容
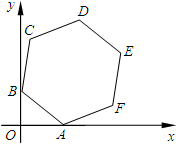
如图，半径长为2的正六边形ABCDEF的顶点A在y轴上，边BC在x轴上，则点E的坐标是______．
取正六边形ABCDEF的中心G，连接AG，DG，FG，EG，EC，
∴∠AGF=∠EGF=∠EGD=60°，
∴A，G，D共线，
∵AG=FG=EG=GD，
∴△AFG，△EGF，△DGE是等边三角形，
∵半径长为2的正六边形ABCDEF的顶点A在y轴上，
∴AG=EG=ED=GD=2，
∵AD⊥EC，
∴GH=
GD=1，
∴AH=3，
即OC=3，
∵EH=
=
，
∴EC=2
，
∴点E的坐标是：（3，2
）．
故答案为：（3，2
）．
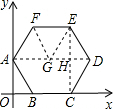
∴∠AGF=∠EGF=∠EGD=60°，
∴A，G，D共线，
∵AG=FG=EG=GD，
∴△AFG，△EGF，△DGE是等边三角形，
∵半径长为2的正六边形ABCDEF的顶点A在y轴上，
∴AG=EG=ED=GD=2，
∵AD⊥EC，
∴GH=
| 1 |
| 2 |
∴AH=3，
即OC=3，
∵EH=
| EG2-GH2 |
| 3 |
∴EC=2
| 3 |
∴点E的坐标是：（3，2
| 3 |
故答案为：（3，2
| 3 |
练习册系列答案
相关题目
