题目内容
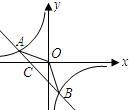
如图,梯形AOBC的顶点A,C在反比例函数图象上,OA∥BC,上底边OA在直线y=x上,下底边BC交x轴于E(2,0),则四边形AOEC的面积为( )

| A.3 | B.
| C.
| D.
|

因为AO∥BC,上底边OA在直线y=x上,
则可设BE的解析式为y=x+b,
将E(2,0)代入上式得,b=-2,
BE的解析式为y=x-2.
把y=1代入y=x-2,得x=3,C点坐标为(3,1),
则反比例函数解析式为y=
,
将它与y=x组成方程组得:
,
解得x=
,x=-
(负值舍去).
代入y=x得,y=
.
A点坐标为(
,
),
OA=
=
,
BC=
=3
,
∵B(0,-2),E(2,0),
∴BE=2
,
∴BE边上的高为
,
∴梯形AOBC高为:
,
梯形AOBC面积为:
×(3
+
)×
=3+
,
△OBE的面积为:
×2×2=2,
则四边形AOEC的面积为3+
-2=1+
.
故选D.

则可设BE的解析式为y=x+b,
将E(2,0)代入上式得,b=-2,
BE的解析式为y=x-2.
把y=1代入y=x-2,得x=3,C点坐标为(3,1),
则反比例函数解析式为y=
| 3 |
| x |
将它与y=x组成方程组得:
|
解得x=
| 3 |
| 3 |
代入y=x得,y=
| 3 |
A点坐标为(
| 3 |
| 3 |
OA=
(
|
| 6 |
BC=
| 32+32 |
| 2 |
∵B(0,-2),E(2,0),
∴BE=2
| 2 |
∴BE边上的高为
| 2 |
∴梯形AOBC高为:
| 2 |
梯形AOBC面积为:
| 1 |
| 2 |
| 2 |
| 6 |
| 2 |
| 3 |
△OBE的面积为:
| 1 |
| 2 |
则四边形AOEC的面积为3+
| 3 |
| 3 |
故选D.


练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 交点.
交点.