题目内容
【题目】（1）如图（1），已知，在△ABC中，AD，AE分别是△ABC的高和角平分线，若∠B=30°，∠C=50°．求∠DAE的度数；
（2）如图（2），已知AF平分∠BAC，交边BC于点E，过F作FD⊥BC，若∠B=x°，∠C=（x+36）°，
①∠CAE= （含x的代数式表示）
②求∠F的度数．
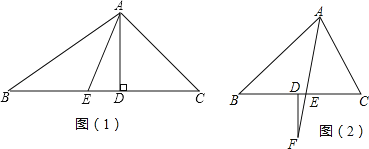
【答案】(1)∠DAE=10°；（2）①72°﹣x°，②∠F=18°．
【解析】试题分析：
(1) 要求∠DAE的度数，可以先求得∠CAE和∠CAD的度数再将它们相减. 先根据三角形的内角和求得∠BAC的度数，再根据AE是∠BAC的角平分线这一条件得到∠CAE的度数. 由于AD是△ABC的高，所以通过直角三角形两锐角的关系可以得到∠CAD的度数. 根据上述角的度数即可求得∠DAE的度数.
(2) 根据三角形的内角和，容易用x表示∠BAC. 根据AF平分∠BAC这一条件，不难用x表示∠CAE和∠BAE. 结合上述结果，利用三角形外角的相关结论，可以得到∠AEC的度数. 根据FD⊥BC，利用对顶角和直角三角形两锐角的关系可以得到∠F的度数.
试题解析：
(1) ∵∠B=30°，∠C=50°，
∴在△ABC中，∠BAC=180°-∠B-∠C=180°-30°-50°=100°.
∵AE是△ABC的角平分线，即AE平分∠BAC，
∴
.
∵AD是△ABC的高，即AD⊥BC，
∴在Rt△ADC中，∠CAD=90°-∠C=90°-50°=40°，
∴∠DAE=∠CAE-∠CAD=50°-40°=10°.
(2) ①∵∠B=x°，∠C=(x+36)°，
∴在△ABC中，∠BAC=180°-∠B-∠C=180°-x°-(x+36)°=(144-2x)°.
∵AF平分∠BAC，
∴
.
故本小题应填写：
.
②∵AF平分∠BAC，
∴∠BAE=∠CAE=72°-x°.
∵∠AEC是△ABE的一个外角，
∴∠AEC=∠BAE+∠B=72°-x°+x°=72°，
∴∠FED=∠AEC=72°.
∵FD⊥BC，
∴在Rt△EDF中，∠F=90°-∠FED=90°-72°=18°.
