题目内容
【题目】数和形是数学的两个主要研究对象,我们经常运用数形结合、数形转化的方法解决一些数学问题.下面我们来探究“由数思形,以形助数”的方法在解决代数问题中的应用.
探究一:求不等式|x﹣1|<2的解集
(1)探究|x﹣1|的几何意义
如图①,在以O为原点的数轴上,设点A′对应的数是x﹣1,有绝对值的定义可知,点A′与点O的距离为
|x﹣1|,可记为A′O=|x﹣1|.将线段A′O向右平移1个单位得到线段AB,此时点A对应的数是x,点B对应的数是1.因为AB=A′O,所以AB=|x﹣1|,因此,|x﹣1|的几何意义可以理解为数轴上x所对应的点A与1所对应的点B之间的距离AB.

(2)求方程|x﹣1|=2的解
因为数轴上3和﹣1所对应的点与1所对应的点之间的距离都为2,所以方程的解为3,﹣1.
(3)求不等式|x﹣1|<2的解集
因为|x﹣1|表示数轴上x所对应的点与1所对应的点之间的距离,所以求不等式解集就转化为求这个距离小于2的点对应的数x的范围.请写出这个解集:_________________________________.
探究二:探究![]() 的几何意义
的几何意义
(1)探究![]() 的几何意义
的几何意义
如图③,在直角坐标系中,设点M的坐标为(x,y),过M作MP⊥x轴于P,作MQ⊥y轴于Q,则P点坐标为(x,0),Q点坐标为(0,y),OP=|x|,OQ=|y|,在Rt△OPM中,PM=OQ=|y|,则![]() ,因此,
,因此,![]() 的几何意义可以理解为点M(x,y)与点O(0,0)之间的距离MO.
的几何意义可以理解为点M(x,y)与点O(0,0)之间的距离MO.

(2)探究![]() 的几何意义
的几何意义
如图④,在直角坐标系中,设点A′的坐标为(x﹣1,y﹣5),由探究二(1)可知,![]() ,将线段A′O先向右平移1个单位,再向上平移5个单位,得到线段AB,此时点A的坐标为(x,y),点B的坐标为(1,5),因为AB=A′O,所以
,将线段A′O先向右平移1个单位,再向上平移5个单位,得到线段AB,此时点A的坐标为(x,y),点B的坐标为(1,5),因为AB=A′O,所以![]() ,因此
,因此![]() 的几何意义可以理解为点A(x,y)与点B(1,5)之间的距离AB.
的几何意义可以理解为点A(x,y)与点B(1,5)之间的距离AB.

(3)探究![]() 的几何意义,根据探究二(2)所得的结论,请写出
的几何意义,根据探究二(2)所得的结论,请写出![]() 的几何意义可以理解为:________________.
的几何意义可以理解为:________________.
(4)![]() 的几何意义可以理解为:________________________________.
的几何意义可以理解为:________________________________.
【答案】探究一(3)![]() ;探究二(3)点A(x,y)与点B(-3,4)之间的距离AB;(4)点A(x,y)与点B(a,b)之间的距离.
;探究二(3)点A(x,y)与点B(-3,4)之间的距离AB;(4)点A(x,y)与点B(a,b)之间的距离.
【解析】
探究一(3)由于|x﹣1|表示数轴上x所对应的点与1所对应的点之间的距离,所以求不等式解集就转化为求这个距离小于2的点对应的数x的范围,从而画出数轴即可;
探究二(3)由于![]() 的几何意义可以理解为点A(x,y)与点B(1,5)之间的距离AB,所以可以得到
的几何意义可以理解为点A(x,y)与点B(1,5)之间的距离AB,所以可以得到![]() 的几何意义是:点A(x,y)与点B(-3,4)之间的距离AB;
的几何意义是:点A(x,y)与点B(-3,4)之间的距离AB;
(4)由前面的探究可知![]() 的几何意义可以理解为:点A(x,y)与点B(a,b)之间的距离.
的几何意义可以理解为:点A(x,y)与点B(a,b)之间的距离.
解:探究一:(3)如图所示,
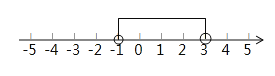
![]() 的解集是
的解集是![]() ;
;
探究二:(3)如图,
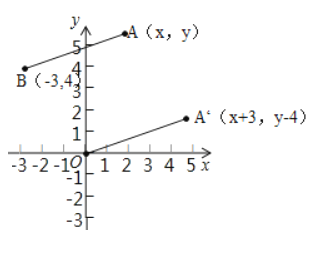
在直角坐标系中,设点A′的坐标为(x+3,y﹣4),
由探究二(1)可知,![]() ,
,
将线段A′O先向左平移3个单位,再向上平移4个单位,得到线段AB,
此时点A的坐标为(x,y),点B的坐标为(-3,4),
∵AB=A′O,
∴![]() ,.
,.
∴![]() 的几何意义是:点A(x,y)与点B(-3,4)之间的距离AB;
的几何意义是:点A(x,y)与点B(-3,4)之间的距离AB;
(4)根据前面的探究可知![]() 的几何意义可以理解为:点A(x,y)与点B(a,b)之间的距离.
的几何意义可以理解为:点A(x,y)与点B(a,b)之间的距离.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案【题目】如图所示,在平面直角坐标系中,平行四边形ABCD的顶点A、D的坐标分别是(0,0),(2,3),AB=5,则顶点C的坐标是( )

A. (3,7)B. (5,3)C. (7,3)D. (8,2)
【题目】某学校的数学小组将七年级学生某个星期天阅读时间t(单位:分钟)的调查数据进行整理,绘制出如下不完整的频数分布表和频数分布直方图;

阅读时间分钟 | 频数(人数) | 频率 |
30≤t<40 | 10 | 5% |
40≤t<50 | 40 | m |
50≤t<60 | a | 40% |
60≤t<70 | b | n |
70≤t<80 | 20 | 10% |
(1)求a=________,b=________,m=________,n=________;
(2)补全频数分布直方图;
(3)如果阅读时间不少于60分钟即为达标,则达标人数共有多少人?若七年级学生在某时间段内阅读的人数有500人,估计约有多少人达标?



