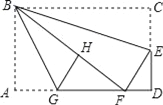
题目内容
【题目】如图,![]() 为
为![]() 轴正半轴上一动点,
轴正半轴上一动点,![]() ,
,![]() ,且
,且![]() 、
、![]() 满足
满足![]() ,
,![]() .
.

(1)求![]() 的面积;
的面积;
(2)若![]() ,
,![]() 、
、![]() 为线段
为线段![]() 上的动点,作
上的动点,作![]() 交
交![]() 于
于![]() ,FP平分∠GFC,FN平分∠AFP交x轴于N,记∠FNB=
,FP平分∠GFC,FN平分∠AFP交x轴于N,记∠FNB=![]() ,求∠BAC(用
,求∠BAC(用![]() 表示);
表示);
(3)若![]() ,
,![]() 轴于
轴于![]() ,点
,点![]() 从
从![]() 点出发,在射线
点出发,在射线![]() 上运动,同时另一动点
上运动,同时另一动点![]() 从点
从点![]() 向
向![]() 点运动,到
点运动,到![]() 停止运动,
停止运动,![]() 、
、![]() 的速度分别为2个单位/秒、3个单位/秒,当
的速度分别为2个单位/秒、3个单位/秒,当![]() 时,求运动的时间.
时,求运动的时间.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)由二次根式和绝对值的非负性可得a、b的值,即可知OA、OB的长,继而可得三角形的面积;
(2)设∠PFC=x、∠AFN=y,由角平分线的定义知∠AFN=∠PFN=y、∠CFP=∠GFP=x,∠AFP=2y、∠GFC=2x,根据∠AFP+∠GFC=180°+∠GFP、∠FNB=∠NFP+∠PFC+∠ACB列出关于x、y的方程组,解之求得x,从而得出∠GFC度数,继而由平行线的性质可得答案;
(3)过![]() 作
作![]() 于
于![]() ,利用面积法求出OG=
,利用面积法求出OG=![]() ,设运动时间为
,设运动时间为![]() 秒,由题意可得
秒,由题意可得![]() ,
,![]() ,
,![]() ,根据三角形的面积公式列式表示
,根据三角形的面积公式列式表示![]() 和
和![]() ,由已知
,由已知![]() 可得关于t的方程,解方程即可求解.
可得关于t的方程,解方程即可求解.
解:(1)∵![]() ,
,
∴a-6=0且b+8=0,
解得:a=6、b=-8,
∴OA=6、OB=8,
则S△AOB=![]() ×OA×OB=
×OA×OB=![]() ×6×8=24;
×6×8=24;
(2)设∠PFC=x、∠AFN=y,
∵FP平分∠GFC,FN平分∠AFP,
∴∠AFN=∠PFN=y、∠CFP=∠GFP=x,∠AFP=2y、∠GFC=2x,
由∠AFP+∠GFC=180°+∠GFP、∠FNB=∠NFP+∠PFC+∠ACB知,![]() ,
,
整理,得:![]() ,
,
解得:![]() ,
,
则∠GFC=2x=4α-600,
∵GF∥AB,
∴∠BAC=∠GFC=4α-600;
(3)过![]() 作
作![]() 于
于![]() ,则
,则![]() ,设运动时间为
,设运动时间为![]() 秒,
秒,
由题意得![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 或
或![]() ,
,
∴![]() 或
或![]() .
.
故答案为:(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案【题目】一家蔬菜公司收购到某种绿色蔬菜200吨,准备加工后进行销售,销售后获利的情况如下表所示:
销售方式 | 粗加工后销售 | 精加工后销售 |
每吨获利(元) | 500 | 800 |
已知该公司的加工能力是:每天能精加工5吨或粗加工15吨,但两种加工不能同时进行.受季节等条件的限制,公司必须在一定时间内将这批蔬菜全部加工后销售完.
(1)如果要求20天刚好加工完200吨蔬菜,则公司应安排几天精加工,几天粗加工?
(2)如果先进行精加工,然后进行粗加工.
①试求出销售利润W元与精加工的蔬菜吨数m之间的函数关系式;
②若要求在不超过16天的时间内,将200吨蔬菜全部加工完后进行销售,则加工这批蔬菜最多获得多少利润?此时如何分配加工时间?