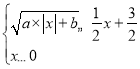题目内容
【题目】某校数学课外小组，在坐标纸上为学校的一块空地设计植树方案如下：第k棵树种植在点Pk(xk，yk)处，其中x1＝1，y1＝2，当k≥2时，xk＝xk﹣1+1﹣5（[
]﹣[
]），yk＝yk﹣1+[]﹣[]，[a]表示非负实数a的整数部分，例如[2.6]＝2，[0.2]＝0．按此方案，第2017棵树种植点的坐标为（ ）
A.(5，2017)B.(6，2016)C.(1，404)D.(2，404)
【答案】D
【解析】
根据规律找出种植点横坐标及纵坐标的表示规律，代入2017即可求得种植点的坐标．
解：∵[
]﹣[
]组成的数为
1，0，0，0，0，1，0，0，0，0，1，0，0，0，0，1…，
将k＝1，2，3，4，5，…，
一一代入计算得xn为
1，2，3，4，5，1，2，3，4，5，1，2，3，4，5，…
即xn的重复规律是x5n+1＝1，x5n+2＝2，x5n+3＝3，x5n+4＝4，x5n＝5．
∴{yn}为1，1，1，1，1，2，2，2，2，2，3，3，3，3，3，4，4，4，4，4，…
即yn的重复规律是y5n+k＝n，0≤k＜5．
∴y2017=y5×403+2=404
∴由题意可知第2017棵树种植点的坐标应（2，404）．
故选：D．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
相关题目
