Question

【题目】综合与探究

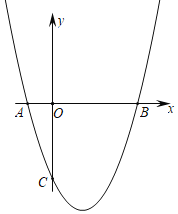
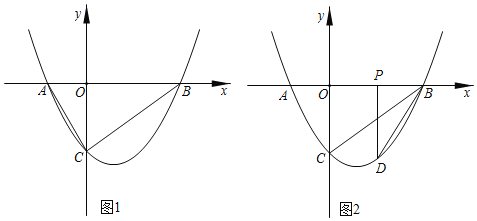
如图1，抛物线与轴交于，两点，与轴交于点．

（1）求抛物线的表达式；

（2）点是抛物线上异于点的动点，若的面积与的面积相等，求出点的坐标；

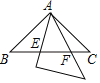
（3）如图2，当为的中点时，过点作轴，交抛物线于点.连接，将沿轴向左平移个单位长度（），将平移过程中与重叠部分的面积记为，求与的函数关系式．

Answer 1

【答案】（1）；（2），，；（3）．

【解析】

（1）利用待定系数法进行求解即可；

（2）先求出点C的坐标，继而可得点N的纵坐标为3或-3，分别代入函数解析式进行求解即可 ；

（3）如图2-2，将沿轴向左平移个单位长度后得到的三角形记作△PQM， PM与BC交于点E，QM与BC交于点F，连接CD，先求出直线BC的解析式，由已知可得，继而得出，求出点E的坐标，点D的坐标，表示出EP、EM的长，过点作于点，证明，得到，再证明，继而利用相似三角形的性质以及比例的性质得到，进而得到，表示出，再由进行求解即可．

（1）∵抛物线经过点，，

∴，

∴，

∴抛物线的表达式为；

（2）将代入，得，

∴点的坐标为，

∴，

设点，

∵，

∴，

∴，

当时，，

解得，．

当时，，

解得，（舍去），

∴，，；

（3）如图2-2，将沿轴向左平移个单位长度后得到的三角形记作△PQM， PM与BC交于点E，QM与BC交于点F，连接CD，

由已知得，，，

设直线的表达式为，

∵直线经过点，，

∴，解得，

∴直线的表达式为，

当时，由已知得，

∴，

当x=2-m时，，

∴，

当时，=-3，

∴点，点M的纵坐标为-3，

∴直线轴，

∵，，

∴，

过点作于点，则，

∵，

∴，

∴，即，

∵CD//OB，

∴，，

∴，

∴，

∵，

∴，

∴，

设，，

∴，

∴，

∴，

∴，

∴，

∵，

∴

．