题目内容
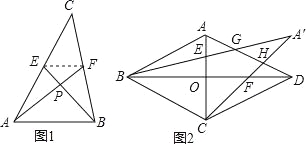
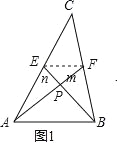
【题目】(2016湖南省邵阳市第25题)尤秀同学遇到了这样一个问题：如图1所示，已知AF，BE是△ABC的中线，且AF⊥BE，垂足为P，设BC=a，AC=b，AB=c．
求证：a2+b2=5c2
该同学仔细分析后，得到如下解题思路：
先连接EF，利用EF为△ABC的中位线得到△EPF∽△BPA，故
，设PF=m，PE=n，用m，n把PA，PB分别表示出来，再在Rt△APE，Rt△BPF中利用勾股定理计算，消去m，n即可得证
（1）请你根据以上解题思路帮尤秀同学写出证明过程．
（2）利用题中的结论，解答下列问题：
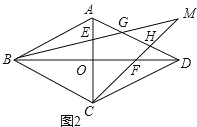
在边长为3的菱形ABCD中，O为对角线AC，BD的交点，E， F分别为线段AO，DO的中点，连接BE，CF并延长交于点M，BM，CM分别交AD于点G，H，如图2所示，求MG2+MH2的值．
【答案】(1)、证明过程见解析；(2)、5
【解析】
试题分析：(1)、设PF=m，PE=n，连结EF，如图1，根据三角形中位线性质得EF∥AB，EF=
c，则可判断△EFP∽△BPA，利用相似比得到PB=2n，PA=2m，接着根据勾股定理得到n2+4m2=
b2，m2+4n2=a2，则5（n2+m2）=（a2+b2），而n2+m2=EF2=c2，所以a2+b2=5c2；(2)、利用（1）的结论得MB2+MC2=5BC2=5×32=45，再利用△AEG∽△CEB可计算出AG=1，同理可得DH=1，则GH=1，然后利用GH∥BC，根据平行线分线段长比例定理得到MB=3GM，MC=3MH，然后等量代换后可得MG2+MH2=5．
试题解析：(1)、设PF=m，PE=n，连结EF，如图1， ∵AF，BE是△ABC的中线，
∴EF为△ABC的中位线，AE=b，BF=a， ∴EF∥AB，EF=c，
∴△EFP∽△BPA， ∴
，即
=
=
， ∴PB=2n，PA=2m，
在Rt△AEP中，∵PE2+PA2=AE2， ∴n2+4m2=
b2①，
在Rt△AEP中，∵PF2+PB2=BF2， ∴m2+4n2=a2②，
①+②得5（n2+m2）=（a2+b2），
在Rt△EFP中，∵PE2+PF2=EF2， ∴n2+m2=EF2=c2， ∴5c2=（a2+b2）， ∴a2+b2=5c2；
(2)、∵四边形ABCD为菱形， ∴BD⊥AC， ∵E，F分别为线段AO，DO的中点，
由（1）的结论得MB2+MC2=5BC2=5×32=45， ∵AG∥BC， ∴△AEG∽△CEB， ∴
=
=
， ∴AG=1，
同理可得DH=1， ∴GH=1， ∴GH∥BC， ∴
=
=
=
，
∴MB=3GM，MC=3MH， ∴9MG2+9MH2=45， ∴MG2+MH2=5．
