Question

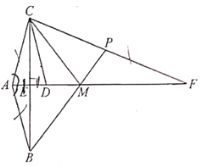
【题目】如图，用尺规作的平分线的方法如下：以为圆心，任意长为半径画弧交，于点，，再分別以点，为圆心，大于的长为半径画弧，两弧交于点，作射线.由作法得，从而得两角相等.那么这两个三角形全等的根据是（ ）

A.B.C.D.

Answer 1

【答案】B

【解析】

认真阅读作法，从角平分线的作法得出△OCP与△ODP的两边分别相等，加上公共边相等，于是两个三角形符合SSS判定方法要求的条件，答案可得．

解：∵以O为圆心，任意长为半径画弧交OA，OB于C，D，即OC=OD；
以点C，D为圆心，以大于长为半径画弧，两弧交于点P，即CP=DP；

∴在△OCP和△ODP中

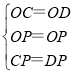
∴△OCP≌△ODP（SSS）．
故选：B．

本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．