题目内容
【题目】如图，一次函数y=﹣ 
x+1的图象与x轴、y轴分别交于点A、B，以线段AB为边在第一象限内作等边△ABC．
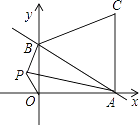
（1）求△ABC的面积；
（2）如果在第二象限内有一点P（a， 
），请用含a的式子表示四边形ABPO的面积，并求出当△ABP的面积与△ABC的面积相等时a的值．
【答案】
（1）解：y=﹣ 
x+1与x轴、y轴交于A、B两点，
∴A（ 
，0），B（0，1）．
∵△AOB为直角三角形，
∴AB=2．
∴S△ABC= 
×2×sin60°=
（2）解：S四边形ABPO=S△ABO+S△BOP= ×OA×OB+ ×OB×h= × ×1+ ×1×|a|．
∵P在第二象限，∴S四边形ABPO= 
﹣ 
= 
，
S△ABP=SABPO﹣S△AOP=（ ﹣ ）﹣ ×OA× ．
∴S△ABP= ﹣ ﹣ 
= ﹣ =S△ABC= ．
∴a=﹣ 
【解析】（1）首先令x=0，y=0求出一次函数的解析式．然后根据勾股定理求出AB的长，继而可求出三角形ABC的面积．（2）依题意可得出S四边形ABPO=S△ABO+S△BOP，当S△ABP=S△ABC时求出a值．
夺冠金卷全能练考系列答案
【题目】在太空种子种植体验实践活动中，为了解“宇番2号”番茄，某校科技小组随机调查60株番茄的挂果数量x（单位：个），并绘制如下不完整的统计图表：
“宇番2号”番茄挂果数量统计表
挂果数量x（个） | 频数（株） | 频率 |
25≤x＜35 | 6 | 0.1 |
35≤x＜45 | 12 | 0.2 |
45≤x＜55 | a | 0.25 |
55≤x＜65 | 18 | b |
65≤x＜75 | 9 | 0.15 |
请结合图表中的信息解答下列问题：
（1）统计表中，a= ，b= ；
（2）将频数分布直方图补充完整；
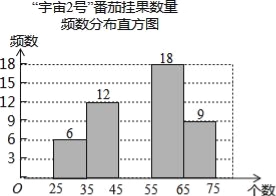
（3）若绘制“番茄挂果数量扇形统计图”，则挂果数量在“35≤x＜45”所对应扇形的圆心角度数为 °；
（4）若所种植的“宇番2号”番茄有1000株，则可以估计挂果数量在“55≤x＜65”范围的番茄有 株．
