题目内容
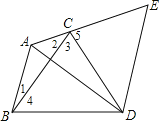
【题目】已知:如图,在△ABC中,∠BAC=1200,以BC为边向形外作等边三角形△BCD,把△ABD绕着点D按顺时针方向旋转600后得到△ECD,若AB=3,AC=2,求∠BAD的度数与AD的长.

【答案】(1)60°;(2)5.
【解析】
试题分析:根据等边三角形的性质由△BCD为等边三角形得到∠3=∠4=60°,DC=DB,再根据旋转的性质得到∠5=∠1+∠4=∠1+60°,则∠2+∠3+∠5=∠2+∠1+120°,再根据三角形内角和定理得到
∠1+∠2=180°-∠BAC=60°,于是∠2+∠3+∠5=60°+120°=180°,即可得到点A、C、E在一条直线上;
由于点A、C、E在一条直线上,△ABD绕着点D按顺时针方向旋转60°后得到△ECD,则∠ADE=60°,DA=DE,得到△ADE为等边三角形,则∠DAE=60°,然后利用∠BAD=∠BAC-∠DAE计算即可;
由于点A、C、E在一条直线上,则AE=AC+CE,根据旋转的性质得到CE=AB,则AE=AC+AB=2+3=5,而△ADE为等边三角形,则AD=AE=5.
试题解析:∵△BCD为等边三角形,∴∠3=∠4=60°,DC=DB,∵△ABD绕着点D按顺时针方向旋转60°后得到△ECD,∴∠5=∠1+∠4=∠1+60°,∴∠2+∠3+∠5=∠2+∠1+120°,∵∠BAC=120°,
∴∠1+∠2=180°-∠BAC=60°,∴∠2+∠3+∠5=60°+120°=180°,∴点A、C、E在一条直线上;∵点A、C、E在一条直线上,而△ABD绕着点D按顺时针方向旋转60°后得到△ECD,∴∠ADE=60°,DA=DE,
∴△ADE为等边三角形,∴∠DAE=60°,∴∠BAD=∠BAC-∠DAE=120°-60°=60°;
∵点A、C、E在一条直线上,∴AE=AC+CE,∵△ABD绕着点D按顺时针方向旋转60°后得到△ECD,
∴CE=AB,∴AE=AC+AB=2+3=5,∵△ADE为等边三角形,∴AD=AE=5.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案