题目内容
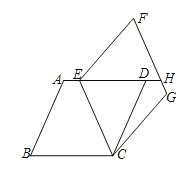
【题目】如图,完全相同的两个菱形ABCD和ECGF的顶点C重合,∠B=∠F,点E恰好在边AD上,延长ED交FG于点H.
(1)求证:∠B=∠ECB;
(2)连接BE、CH.
①试判断四边形BEHC的形状,并说理理由;
②求证:CH平分∠DCG.
【答案】(1)证明见解析,(2)①四边形BEHC是平行四边形,理由见解析,②证明见解析.
【解析】
(1)过A作AN![]() BC于N,作EM
BC于N,作EM![]() BC于M,利用菱形的性质,证明
BC于M,利用菱形的性质,证明![]() 即可得到结论,
即可得到结论,
(2)①利用菱形的性质与∠B=∠F,证明![]() 即可得到结论,
即可得到结论,
②延长BC交FG的延长线于K,证明四边形![]() 是菱形,再证明
是菱形,再证明![]() 利用菱形的性质证明
利用菱形的性质证明![]() 再利用三角形的内角和可得结论.
再利用三角形的内角和可得结论.
证明:(1)如图,过A作AN![]() BC于N,作EM
BC于N,作EM![]() BC于M,
BC于M,
![]() 完全相同的两个菱形ABCD和ECGF,
完全相同的两个菱形ABCD和ECGF,
![]()
![]()
![]()
![]()

(2)①四边形BEHC是平行四边形,理由如下:
如图,连接BE,CH,
![]() 完全相同的两个菱形ABCD和ECGF,
完全相同的两个菱形ABCD和ECGF,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 四边形BEHC是平行四边形
四边形BEHC是平行四边形

②如图,延长BC交FG的延长线于K,
![]()
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]()
![]() 四边形
四边形![]() 是菱形,
是菱形,
![]()
![]()
![]()
![]()
![]()
![]() 完全相同的两个菱形ABCD和ECGF,
完全相同的两个菱形ABCD和ECGF,
![]()
![]()
![]()
![]()
![]() 平分
平分![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】珠海市水务局对某小区居民生活用水情况进行了调査.随机抽取部分家庭进行统计,绘制成如下尚未完成的频数分布表和频率分布直方图.请根据图表,解答下列问题:
月均用水量(单位:吨 | 频数 | 频率 |
2≤x<3 | 4 | 0.08 |
3≤x<4 | a | b |
4≤x<5 | 14 | 0.28 |
5≤x<6 | 9 | c |
6≤x<7 | 6 | 0.12 |
7≤x<8 | 5 | 0.1 |
合计 | d | 1.00 |

(1)b= ,c= ,并补全频数分布直方图;
(2)为鼓励节约用水用水,现要确定一个用水量标准P(单位:吨),超过这个标准的部分按1.5倍的价格收费,若要使60%的家庭水费支出不受影响,则这个用水量标准P= 吨;
(3)根据该样本,请估计该小区400户家庭中月均用水量不少于5吨的家庭约有多少户?