题目内容
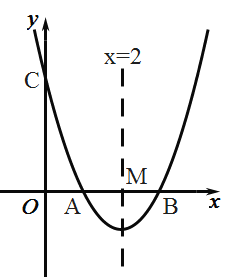
【题目】已知函数![]() (
(![]() ,
,![]() 为常数)的图象经过点
为常数)的图象经过点![]() .
.
(1)求![]() ,
,![]() 满足的关系式;
满足的关系式;
(2)设该函数图象的顶点坐标是![]() ,当
,当![]() 的值变化时,求
的值变化时,求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)若该函数的图象不经过第三象限,当![]() 时,函数的最大值与最小值之差为16,求
时,函数的最大值与最小值之差为16,求![]() 的值.
的值.
【答案】(1)c=2b(2)![]() (3)2或6
(3)2或6
【解析】
(1)把点![]() 代入函数即可得到结论;
代入函数即可得到结论;
(2)根据顶点坐标即可求解;
(3)把函数化为![]() ,根据图像不经过第三象限进行分类讨论进行求解.
,根据图像不经过第三象限进行分类讨论进行求解.
(1)将点![]() 代入
代入![]() ,
,
得![]() ,
,
∴![]() ;
;
(2)![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
(3)![]() ,
,
对称轴![]() ,
,
当![]() 时,
时,![]() ,函数不经过第三象限,则
,函数不经过第三象限,则![]() ;
;
此时![]() ,当
,当![]() 时,函数最小值是0,最大值是25,
时,函数最小值是0,最大值是25,
∴最大值与最小值之差为25;(舍去)
当![]() 时,
时,![]() ,函数不经过第三象限,则
,函数不经过第三象限,则![]() ,
,
∴![]() ,
,
∴![]() ,
,
当![]() 时,函数有最小值
时,函数有最小值![]() ,
,
当![]() 时,函数有最大值
时,函数有最大值![]() ,
,
当![]() 时,函数有最大值
时,函数有最大值![]() ;
;
函数的最大值与最小值之差为16,
当最大值![]() 时,
时,![]() ,
,
∴![]() 或
或![]() ,
,
∵![]() ,
,
∴![]() ;
;
当最大值![]() 时,
时,![]() ,
,
∴![]() 或
或![]() ,
,
∵![]() ,
,
∴![]() ;
;
综上所述![]() 或
或![]() ;
;

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目