题目内容
【题目】如图，已知直线AC∥BD，直线AB，CD不平行，点P在直线AB上，且和点A、B不重合．
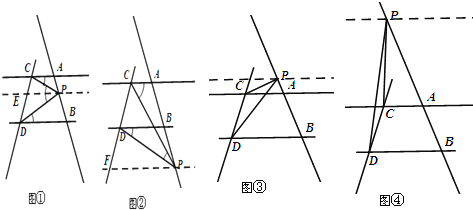
（1）如图①，当点P在线段AB上时，若∠PCA=20°，∠PDB=30°，求∠CPD的度数；
（2）当点P在A、B两点之间运动时，∠PCA，∠PDB，∠CPD 之间满足什么样的等量关系？（直接写出答案）
（3）如图②，当点P在线段AB延长线上运动时，∠PCA，∠PDB，∠CPD 之间满足什么样的等量关系？并说明理由．
（4）当点P在线段BA延长线上运动时，∠PCA，∠PDB，∠CPD 之间满足什么样的等量关系？（直接写出答案）
【答案】（1）50°；（2）∠CPD=∠PCA+∠PDB；（3）∠CPD=∠CPF﹣∠DPF=∠PCA﹣∠PDB；（4）见解析
【解析】
试题分析：（1）如图①，过P点作PE∥AC交CD于E点，由于AC∥BD，则PE∥BD，根据平行线的性质得∠CPE=∠PCA=20°，∠DPE=∠PDB=30°，所以∠CPD=50°；
（2）证明方法与（1）一样；
（3）如图②，过P点作PF∥BD交CD于F点，由于AC∥BD，则PF∥AC，根据平行线的性质得∠CPF=∠PCA，∠DPF=∠PDB，所以∠CPD=∠PCA﹣∠PDB；
（4）如图③和④，类似（3）的说明方法易得∠PCA，∠PDB，∠CPD 之间满足什么样的等量关系．
解：（1）如图①，过P点作PE∥AC交CD于E点，
∵AC∥BD
∴PE∥BD，
∴∠CPE=∠PCA=20°，∠DPE=∠PDB=30°，
∴∠CPD=∠CPE+∠DPE=50°；
（2）∠CPD=∠PCA+∠PDB（证明方法与（1）一样；
（3）∠CPD=∠PCA﹣∠PDB．理由如下：
如图②，过P点作PF∥BD交CD于F点，
∵AC∥BD，
∴PF∥AC，
∴∠CPF=∠PCA，∠DPF=∠PDB，
∴∠CPD=∠CPF﹣∠DPF=∠PCA﹣∠PDB；
（4）如图③，∠CPD=∠PDB﹣∠PCA；
如图④，∠CPD=∠PCA﹣∠PDB．
（证明方法与（3）类似．
