Question

【题目】如图，是的直径，且，点为的延长线上一点，过点作的切线、，切点分别为、．

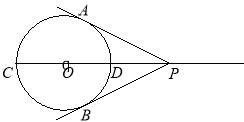
（1）、连接,若，试证明是等腰三角形；

（2）、填空：①当= 时，四边形是菱形；②当= 时，四边形是正方形．

Answer 1

【答案】（1）、证明过程见解析；（2）、1；－1

【解析】

试题分析：（1）、连接OA、AC。根据切线的性质可得：∠OAP=90°，根据三角形内角和定理可得∠AOP=60°，根据等腰三角形的性质以及外角的性质可得：∠ACP=∠CAO=30°，从而得到三角形的形状；（2）、根据菱形和正方形的性质得出线段的长度.

试题解析：（1）、连接OA、AC ∵PA为⊙O的切线，∴OA⊥PA.

在Rt△AOP中，∠AOP=90°－∠APO=90°-30°=60°. ∴∠ACP=∠AOP=×60°=30°

∴∠ACP=∠APO, ∴AC=AP. ∴△ACP是等腰三形.

（2）、①1；②-1.