题目内容

已知直角三角形两条直角边的和等于8，两条直角边各为多少时，这个直角三角形的面积最大，最大值是多少？

分析：先求出面积和直角边间的数量关系，再利用二次函数的顶点坐标求出面积的最大值．

解答：解：设直角三角形的直角边为x，则另一直角边为8-x．直角三角形的面积是S．
根据题意，得
S=

x（8-x）（0＜x＜8），
配方，得
S=-

（x-4）²+8；
∴当x=4时，即两条直角边各为4时，此时三角形的面积最大，最大面积是8．

点评：本题考查了二次函数的最值．求二次函数的最值时，本题采用了配方法．

练习册系列答案

1加1阅读好卷系列答案

相关题目

学习过三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化．类似的，也可以在等腰三角形中建立边角之间的联系，我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad）．如图，在△ABC中，AB=AC，顶角A的正对记作sadA，这时sad A= $数学公式$ ．容易知道一个角的大小与这个角的正对值也是相互唯一确定的．
根据上述对角的正对定义，解下列问题：
（1）填空：sad60°=，sad90°=，sad120°=；
（2）对于0°＜A＜180°，∠A的正对值sadA的取值范围是；
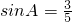（3）如图，已知 $数学公式$ ，其中A为锐角，试求sadA的值；
（4）设sinA=k，请直接用k的代数式表示sadA的值为__．

试题分类