题目内容
如图(1),四边形ABCD内部有一点P,使得S△APD+S△BPC=S△PAB+S△PCD,那么这样的点P叫做四边形ABCD的等积点.(1)如果四边形ABCD内部所有的点都是等积点,那么这样的四边形叫做等积四边形.
①请写出你知道的等积四边形:
②如图(2),若四边形ABCD是平行四边形且S△ABP=8,S△APD=7,S△BPC=15,则S△PCD=
(2)如图(3),等腰梯形ABCD,AD=4,BC=10,AB=5,直线l为等腰梯形的对称轴,分别交AD于点E,交BC于点F.
①请在直线l上找到等腰梯形的等积点,并求出PE的长度.
②请找出等腰梯形ABCD内部所有的等积点,并画图表示.

分析:(1)①过O作EF⊥BC于F,交AD于E,根据平行四边形的性质和 三角形的面积求出S△OAD+S△OBC=
S平行四边形ABCD即可;②根据已知公式代入求出即可;
(2)①作AR⊥BC于R,DT⊥BC于T,根据勾股定理求出AR,计算等腰梯形的面积,根据已知得到∴
×AD×PE+
×BC×(4-PE)=14,求出即可;②根据求出的PE=2,计算PF=PE=2,根据梯形的中位线定理即可得到答案.
| 1 |
| 2 |
(2)①作AR⊥BC于R,DT⊥BC于T,根据勾股定理求出AR,计算等腰梯形的面积,根据已知得到∴
| 1 |
| 2 |
| 1 |
| 2 |
解答:(1)①解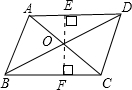
过O作EF⊥BC于F,交AD于E,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵EF⊥BC,
∴EF⊥AD,
∴S△OAD+S△OBC=
×AD×OE+
×BC×OF=
BC×EF=
S平行四边形ABCD,
同理S△OAB+S△OCD=
S平行四边形ABCD,
∴S△OAB+S△OCD=S△OAD+S△OBC,
∴平行四边形ABCD符合条件,
同理:正方形、矩形、菱形都符合,
故答案为:正方形、矩形、菱形、平行四边形.
②解:∵四边形ABCD是平行四边形且S△ABP=8,S△APD=7,S△BPC=15,
∴S△PCD+S△PAB=S△PAD+S△PBC,
∴S△PCD=7+15-8=14,
故答案为:14.
(2)①解:作AR⊥BC于R,DT⊥BC于T,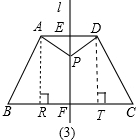
∵等腰梯形ABCD,
∴BR=TC=
(BC-AD)=3,
由勾股定理得:AR=DT=
=4,
∴等腰梯形ABCD的面积是
×(AD+BC)×AR=
×(4+10)×4=28,
∴S△PAD+S△PBC=
×28=14,
∴
×AD×PE+
×BC×(4-PE)=14,
解得:PE=2,
答:PE的长是2.
②解过P作HK∥AD交AB于H,交CD于K,
即作等腰梯形的中位线HK,
则等腰梯形ABCD内部所有的等积点是线段HK上任意一点都符合(端点H、K除外),如图.

过O作EF⊥BC于F,交AD于E,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵EF⊥BC,
∴EF⊥AD,
∴S△OAD+S△OBC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
同理S△OAB+S△OCD=
| 1 |
| 2 |
∴S△OAB+S△OCD=S△OAD+S△OBC,
∴平行四边形ABCD符合条件,
同理:正方形、矩形、菱形都符合,
故答案为:正方形、矩形、菱形、平行四边形.
②解:∵四边形ABCD是平行四边形且S△ABP=8,S△APD=7,S△BPC=15,
∴S△PCD+S△PAB=S△PAD+S△PBC,
∴S△PCD=7+15-8=14,
故答案为:14.
(2)①解:作AR⊥BC于R,DT⊥BC于T,

∵等腰梯形ABCD,
∴BR=TC=
| 1 |
| 2 |
由勾股定理得:AR=DT=
| AB2-BR2 |
∴等腰梯形ABCD的面积是
| 1 |
| 2 |
| 1 |
| 2 |
∴S△PAD+S△PBC=
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
解得:PE=2,

答:PE的长是2.
②解过P作HK∥AD交AB于H,交CD于K,
即作等腰梯形的中位线HK,
则等腰梯形ABCD内部所有的等积点是线段HK上任意一点都符合(端点H、K除外),如图.
点评:本题主要考查对等腰梯形的性质,平行四边形的性质,三角形的面积,三角形的中位线定理,勾股定理,解一元一次方程等知识点的理解和掌握,能综合运用这些性质进行计算是解此题的关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
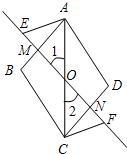 56、如图,O为平行四边形ABCD的对角线AC的中点,过点O作一条直线分别与AB,CD交于点M,N,点E,F在直线MN上,且OE=OF.
56、如图,O为平行四边形ABCD的对角线AC的中点,过点O作一条直线分别与AB,CD交于点M,N,点E,F在直线MN上,且OE=OF. 18、如图,已知平行四边形ABCD.
18、如图,已知平行四边形ABCD.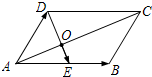 如图,已知平行四边形ABCD,E是边AB的中点,连接AC、DE交于点O.记向量
如图,已知平行四边形ABCD,E是边AB的中点,连接AC、DE交于点O.记向量 画出如图所示的平行四边形ABCD绕点D顺时针旋转90°后的图形,再经几次90°旋转可以与原来图形重合.
画出如图所示的平行四边形ABCD绕点D顺时针旋转90°后的图形,再经几次90°旋转可以与原来图形重合.