题目内容
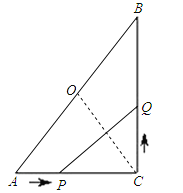
【题目】如图，在Rt△ABC中，∠ACB=90°，AC=10cm，BC=15cm，点P从A出发沿AC向C点以1厘米/秒的速度匀速移动；点Q从C出发沿CB向B点以2厘米/秒的速度匀速移动．点P、Q分别从起点同时出发，移动到某一位置时所需时间为t秒
当t = 4时，求线段PQ的长度
(2)当t为何值时，△PCQ是等腰三角形？
（3）当t为何值时，△PCQ的面积等于16cm2？
（4）当t为何值时，△PCQ∽△ACB
【答案】见解析
【解析】试题分析：（1）由于点P从A出发沿AC向C点以1厘米/秒的速度匀速移动，点Q从C出发沿CB向B点以2厘米/秒，而t=4，由此可以用t表示AP、PC、CQ的长度，然后利用勾股定理即可求出PQ的长度；
（2）令PC＝CQ，求t的值.
（3）首先用t分别表示CP，CQ的长度，然后利用三角形的面积公式即可列出关于t的方程，解方程即可解决问题；
（4）利用直角三角形的斜边中点的性质可以证明△ABC和△PCQ相似，再根据相似三角形的性质，求得t的值.
试题解析：
（1）当t=4时，
∵点P从A出发沿AC向C点以1厘米/秒的速度匀速移动，点Q从C出发沿CB向B点以2厘米/秒的速度匀速移动，
∴AP=4cm，PC=AC﹣AP=6cm、CQ=2×4=8cm，
∴PQ=
=10cm；
（2）∵AP=t，PC=AC﹣AP=10﹣t、CQ=2t，
当PC＝CQ时
10-t=2t
t=
（3）∵AP=t，PC=AC﹣AP=10﹣t、CQ=2t，
∴S△PQC=
PC×CQ=t（10﹣t）=16，
∴t1=2，t2=8，当t=8时，CQ=2t=16＞15，
∴舍去，
∴当t=2时，△PQC的面积等于16cm2；
（4）∵点O为AB的中点，∠ACB=90°，
∴OA=OB=OC（直角三角形斜边上中线定理），
∴∠A=∠OCA，
而∠OCA+∠QPC=90°，∠A+∠B=90°，
∴∠B=∠QPC，又∠ACB=∠PCQ=90°，
∴△ABC∽△QPC,
∴
∴t=2.5s．
