Question

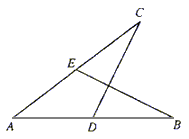
已知如图所示，AB＝AE，∠BAE＝∠CAD，AC＝AD．求证BC＝ED．

Answer 1

答案：
解析：

证明：∵∠BAE＝∠CAD(已知)， 　　∴∠BAE＋∠EAC＝∠CAD＋∠EAC(等量加等量和相等)， 　　即∴∠BAC＝∠EAD， 　　在△ABC和△AED中， 　　∵AB＝AE(已知)， 　　∠BAC＝∠EAD(已证)， 　　AC＝AD(已知)， 　　∴△ABC≌△AED(A．S．A．)． 　　∴BC＝ED(全等三角形的对应边相等)． 　　分析：欲证BC＝ED，只需证△BCA≌△EDA，只需证AB＝AE，AC＝AD，∠BAC＝∠EAD．又∠BAE＝∠CAD(已知)，∠EAC＝∠EAC(公共角)，所以∠BAC＝∠EAD．