题目内容
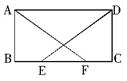
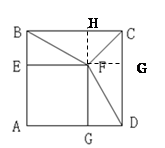
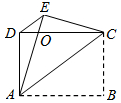
如图,正方形AEFG的顶点E、G在正方形ABCD的边AB、AD上,连接BF、DF.
(1)求证:BF=DF;
(2)连接CF,请直接写出BE∶CF的值(不必写出计算过程).

(1)求证:BF=DF;
(2)连接CF,请直接写出BE∶CF的值(不必写出计算过程).

(1)证明见解析;(2)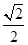 .
.
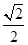 .
.试题分析:(1)由正方形的性质可证△DGF≌△BEF,即证DF=BF.(2)(2)如图,可设AB=3,AE=2,则BE=1;延长GF交BC于点H,延长EF交CD于点G,则四边形FGCH为正方形,CF为这个正方形的对角线,FH为这个正方形的边,所以CF:FH=
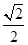 ;又因为FH=BE,所以BE∶CF=
;又因为FH=BE,所以BE∶CF=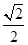 .
.
试题解析:证明:(1)∵四边形ABCD和AEFG都是正方形,
∴AB=AD,AE=AG=EF=FG,∠BEF=∠DGF=90°, 1分
∵BE=AB-AE,DG=AD-AG,∴BE= DG, 2分
∴△BEF≌△DGF.
∴BF=DF. 4分
(2)BE∶CF=
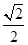 . 6分
. 6分
练习册系列答案
相关题目
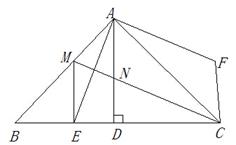
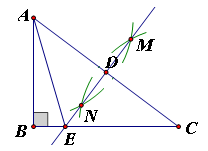
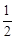 AC长为半径画弧,两弧相交于点M、N,作直线MN,与AC交于点D,与BC交于点E,连接AE.
AC长为半径画弧,两弧相交于点M、N,作直线MN,与AC交于点D,与BC交于点E,连接AE.