题目内容
【题目】我们知道某些代数恒等式可用一些卡片拼成的图形面积来解释,例如:图A可以用来解释![]() ,实际上利用一些卡片拼成的图形面积也可以对某些整式进行乘法运算.
,实际上利用一些卡片拼成的图形面积也可以对某些整式进行乘法运算.



(1)图B可以解释的代数恒等式是_____________ ;
(2)现有足够多的正方形和矩形卡片,如图C:
①若要拼出一个面积为![]() 的矩形,则需要1号卡片 张,2号卡片 张,3号卡片 张;
的矩形,则需要1号卡片 张,2号卡片 张,3号卡片 张;
②试画出一个用若干张1号卡片、2号卡片和3号卡片拼成的矩形,使该矩形的面积为![]() ,并利用你画的图形面积对
,并利用你画的图形面积对![]() 进行乘法运算.
进行乘法运算.
【答案】(1)(m+n)(2n+m)=2n2+3mn+m2;(2)1,2,3.② 2a2+5ab+2b2.
【解析】
(1)看图即可得出所求的式子;
(2)①求出(a+2b)(a+b)的值,即可得出答案;②画出图形,即可得出答案,根据图形和矩形面积公式求出即可.
(1)图B可以解释的代数恒等式是:(m+n)(2n+m)=2n2+3mn+m2,
故答案为:(m+n)(2n+m)=2n2+3mn+m2;
(2)①(a+2b)(a+b)=a2+ab+2ab+2b2=a2+3ab+2b2,
即需要1号卡片1张,2号卡片2张,3号卡片3张,
故答案为:1,2,3.
②如图:
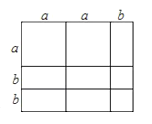
根据图形可知:(2a+b)(a+2b)=2a2+5ab+2b2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目




