Question

【题目】如图所示，已知的直径，延长到，使，过作的切线，为切点，连接、．求：

的长；

的值；

的面积．

Answer 1

【答案】(1)；(2)；(3)．

【解析】

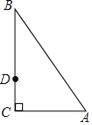
（1）连结OD，根据切线的性质得OD⊥DC，由于BC=AB=1得到OD=，OC=，在中，根据勾股定理即可求得DC=；（2）根据已知条件易证△CDB∽△CAD，根据相似三角形的性质可得DB：DA=CD：CA=：2，由此即可求得AD：BD的值；（3设DB=x，则AD=x，在Rt△ADB中，根据勾股定理可得方程，解得x=，即可得DB，，然后根据三角形面积公式即可求得△ABD的面积．

连结，如图，

∵为的切线，

∴，

∵，

∴，，

在中，；

∵，

而，

∴，

∵为直径，

∴，

∴，

∴，

而公共，

∴，

∴，

∴；

设，则，

在中，，

∵，

∴，

解得，

∴，，

∴的面积．