题目内容
如图,已知?ABCD水平放置在平面直角坐标系xOy中,若点A,D的坐标分别为(-2,5),(0,1),点B(3,5)在反比例函数y= (x>0)图象上.
(x>0)图象上.
(1)求反比例函数y= 的解析式;
的解析式;
(2)将?ABCD沿x轴正方向平移10个单位后,能否使点C落在反比例函数y= 的图象上?并说明理由.
的图象上?并说明理由.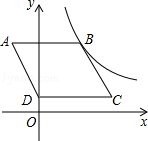
(1)反比例函数的解析式为y= ;
;
(2)平移后的点C能落在y= 的图象上,理由见解析.
的图象上,理由见解析.
解析试题分析:(1)把B(3,5)代入反比例函数解析式可得k的值,进而得到函数解析式;
(2)根据A、D、B三点坐标可得AB=5,AB∥x轴,根据平行四边形的性质得到AB∥CD∥x轴,再由?ABCD沿x轴正方向平移10个单位后C点坐标为(15,1),根据反比例函数图象上点的坐标特点可得点C落在反比例函数y= 的图象上.
的图象上.
试题解析:(1)∵点B(3,5)在反比例函数y= (x>0)图象上,∴k=15,
(x>0)图象上,∴k=15,
∴反比例函数的解析式为y= ;
;
(2)平移后的点C能落在y= 的图象上;理由是:
的图象上;理由是:
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵点A,D的坐标分别为(﹣2,5),(0,1),点B(3,5),
∴AB=5,AB∥x轴,
∴DC∥x轴,
∴点C的坐标为(5,1),
∴?ABCD沿x轴正方向平移10个单位后C点坐标为(15,1),
∴平移后的点C能落在y= 的图象上.
的图象上.
考点:1.平行四边形的性质2.反比例函数图象上点的坐标特征3.待定系数法求反比例函数解析式.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
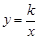 的图象过点A,则k= .
的图象过点A,则k= .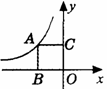
 的图象交于A、B两点,与x轴交于点C,已知点A的坐标为(﹣1,m).
的图象交于A、B两点,与x轴交于点C,已知点A的坐标为(﹣1,m).
 ,
, 与
与 成反比例,
成反比例, 与
与 成正比例,并且当
成正比例,并且当 时,
时, ,当
,当 时,
时, .
. 关于
关于 时,求
时,求 的图象与正比例函数y=kx的图象交于点A(m,﹣2).
的图象与正比例函数y=kx的图象交于点A(m,﹣2).

 的图象与反比例函数
的图象与反比例函数 的图象交于一、三象限内的A、B两点,与x轴交于C点,点A的坐标为(2,m),点B的坐标为(n,
的图象交于一、三象限内的A、B两点,与x轴交于C点,点A的坐标为(2,m),点B的坐标为(n, ),tan∠BOC
),tan∠BOC 。
。
 在第一象限图像上,点A1、A2……An在X轴上,若△P1OA1、△P2A1A2……△PnAN-1AN均为等腰直角三角形,则:
在第一象限图像上,点A1、A2……An在X轴上,若△P1OA1、△P2A1A2……△PnAN-1AN均为等腰直角三角形,则:
 的图象关于y轴成轴对称,则该函数的解析式为 .
的图象关于y轴成轴对称,则该函数的解析式为 .