题目内容
已知抛物线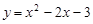 .
.
(1)它与x轴的交点的坐标为_______;
(2)在坐标系中利用描点法画出它的图象;
(3)将该抛物线在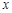 轴下方的部分(不包含与
轴下方的部分(不包含与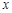 轴的交点)记为G,若直线
轴的交点)记为G,若直线 与G 只有一个公共点,则
与G 只有一个公共点,则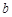 的取值范围是_______.
的取值范围是_______.
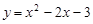 .
.(1)它与x轴的交点的坐标为_______;
(2)在坐标系中利用描点法画出它的图象;
(3)将该抛物线在
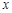 轴下方的部分(不包含与
轴下方的部分(不包含与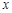 轴的交点)记为G,若直线
轴的交点)记为G,若直线 与G 只有一个公共点,则
与G 只有一个公共点,则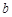 的取值范围是_______.
的取值范围是_______.(1)(-1,0),(3,0)(2),列表,描点,连线及可画图。(3)-3≤b﹤1或b=-

试题分析:(1)∵y=x2-2x-3与x轴相交,y=0,∴x2-2x-3=0,解得x1=-1,x2=3.(2)图像的画法三步骤;列表,连点,连线。(3)∵y=x2-2x-3与y="x+b交于点G," ∴x2-2x-3="x+b" 即x2-3x-3-b="0∴△=9-4(-3-b),即21+4b≥0," ∴b≥-
 ,∵G点在x轴下面,∴x2-2x-3-b≤0 解得-3≤b<1解:(1)它与x轴的交点的坐标为(
,∵G点在x轴下面,∴x2-2x-3-b≤0 解得-3≤b<1解:(1)它与x轴的交点的坐标为(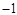 ,0),(3,0); 1分
,0),(3,0); 1分(2)列表:
| x | … | 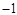 | 0 | 1 | 2 | 3 | … |
| y | … | 0 | 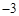 | 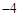 | 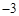 | 0 | … |
(3)
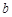 的取值范围是
的取值范围是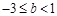 或
或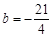 .…5分
.…5分阅卷说明:只写
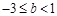 或只写
或只写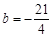 得1分.
得1分.点评:由解析式与x轴相交纵坐标为0,解方程可求出坐标点,根据解析式,可画图像,由于一次函数与二次函数有唯一交点,可列方程,点G又在x轴下,构建不等式求出b的取值范围。属于中档题,注意的是,构建不等式及其解法。

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
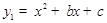 的图象与x轴交于A、B 两点,与
的图象与x轴交于A、B 两点,与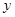 轴交于点C,且点B的坐标为(1,0),点C的坐标为
轴交于点C,且点B的坐标为(1,0),点C的坐标为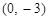 ,一次函数
,一次函数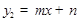 的图象过点A、C.
的图象过点A、C.
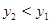 时,
时,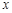 的取值范围.
的取值范围.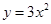 先向上平移3个单位,再向左平移2个单位后得到的抛物线解析式为
先向上平移3个单位,再向左平移2个单位后得到的抛物线解析式为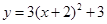

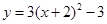
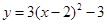
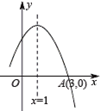
 ,△DCQ的面积为y1平方厘米,△PCQ的面积为y2平方厘米.
,△DCQ的面积为y1平方厘米,△PCQ的面积为y2平方厘米.

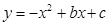 的部分图象如图所示,若
的部分图象如图所示,若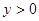 ,则
,则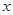 的取值范围是( )
的取值范围是( )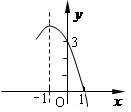
 或
或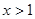
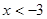 或
或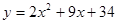 ,当自变量
,当自变量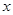 取两个不同的值
取两个不同的值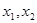 时函数值相等,则当自变量
时函数值相等,则当自变量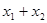 时函数值与( )
时函数值与( )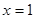 时的函数值相等
时的函数值相等 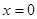 时的函数值相等
时的函数值相等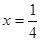 时的函数值相等
时的函数值相等 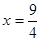 时的函数值相等
时的函数值相等