题目内容
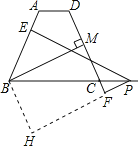
【题目】如图,在等腰梯形 ABCD 中,AD∥BC,AB=CD.点 P 为底边 BC 的延长线上任意一点,PE⊥AB 于 E,PF⊥DC 于 F,BM⊥DC 于 M.请你探究线段 PE、PF、BM 之间的数量关系:
______.

【答案】PE-PF=BM.
【解析】
过点B作BH∥CD,交PF的延长线于点H,易证四边形BMFH是平行四边形,于是有FH=BM,再用AAS证明△PBE≌△PBH,可得PH=PE,继而得到结论.
解:PE-PF=BM. 理由如下:
过点B作BH∥CD,交PF的延长线于点H,如图
∴∠PBH=∠DCB,
∵PF⊥CD,BM⊥CD,
∴BM∥FH,PH⊥BH,
∴四边形BMFH是平行四边形,∠H=90°,
∴FH=BM,
∵等腰梯形ABCD中,AD∥BC,AB=DC,
∴∠ABC=∠DCB,
∴∠ABC=∠PBH,
∵PE⊥AB,
∴∠PEB=∠H=90°,又PB为公共边,
∴△PBE≌△PBH(AAS),
∴PH=PE,
∴PE=PF+FH=PF+BM.
即PE-PF=BM.

练习册系列答案
相关题目
【题目】有![]() 筐白菜,以每筐
筐白菜,以每筐![]() 千克为标准,超过或不足的分别用正、负来表示,记录如下:
千克为标准,超过或不足的分别用正、负来表示,记录如下:
与标准质量的差 |
|
|
|
|
|
|
筐 数 |
|
|
|
|
|
|
(1)与标准质量比较,![]() 筐白菜总计超过或不足多少千克?
筐白菜总计超过或不足多少千克?
(2)若白菜每千克售价![]() 元,则出售这
元,则出售这![]() 筐白菜可卖多少元?
筐白菜可卖多少元?