Question

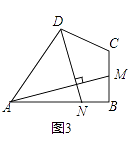
【题目】如图，AB是⊙O的直径，AM、BN分别与⊙O相切于点A、B，CD交AM、BN于点D、C，DO平分∠ADC．
（1）求证：CD是⊙O的切线；
（2）设AD=4，AB=x （x＞0），BC=y （y＞0）．求y关于x的函数解析式．

Answer 1

【答案】
（1）解：过O作OE⊥CD于点E，则∠OED=90°．

∵⊙O与AM相切于点A，

∴∠OAD=90°．

∵OD平分∠ADE，

∴∠ADO=∠EDO．

∵OD=OD，

∴△OAD≌△OED．

∴OE=OA．

∵OA是⊙O的半径，

∴OE是⊙O的半径．

∴CD是⊙O的切线

（2）解：如图2所示：过O作OE⊥CD于点E，过点D作DF⊥BC于点F，则DF=AB=x．

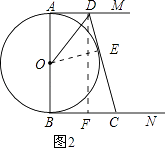
∵AD=4，BC=y，

∴CF=BC﹣AD=y﹣4．

由切线长定理可得：DE=DA，CE=CB，

∴CD=CE+ED

=BC+AD

=4+y

在Rt△DFC中，

∵CD2=DF2+FC2

∴（y+4）=x2+（y﹣4）2．

整理得：y= x2，则y关于x的函数关系式为：y= x2

【解析】（1）过O作OE⊥CD于点E，则∠OED=90°．依据切线的性质可知∠OAD=90°，接下来证明△OAD≌△OED，依据全等三角形的性质可知OA=OE，故此OE为⊙O的半径，则CD是⊙O的切线；（2）如图2所示：过O作OE⊥CD于点E，过点D作DF⊥BC于点F，则DF=AB=x．由切线长定理可得：DE=DA，CE=CB，则CD=4+y，在Rt△DFC中依据勾股定理可得到（y+4）=x2+（y﹣4）2 ， 从而可得到y与x的函数关系式．