Question

【题目】如图，AB是⊙O的直径， = ，且AB=5，BD=4，求弦DE的长．

Answer 1

【答案】解：连接AD， ∵ = ，
∴AD=DE，
又∵AB为直径，
∴∠ADB=90°，
∵AB=5，BD=4，
∴DE=AD= =3，
∴DE的长为3．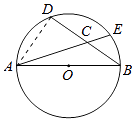

【解析】连接AD，在Rt△ABD中利用勾股定理求出AD，根据等弧对等弦得出AD=DE．
【考点精析】根据题目的已知条件，利用勾股定理的概念和圆心角、弧、弦的关系的相关知识可以得到问题的答案，需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等；在同圆或等圆中，同弧等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．