��Ŀ����
����Ŀ����ͼ��������y=x2+bx+c��ֱ��y= ![]() x��3����A��B���㣬���е�A��y���ϣ���B����Ϊ����4����5������PΪy��������������һ���㣬����P��PC��x���ڵ�C����AB�ڵ�D��
x��3����A��B���㣬���е�A��y���ϣ���B����Ϊ����4����5������PΪy��������������һ���㣬����P��PC��x���ڵ�C����AB�ڵ�D��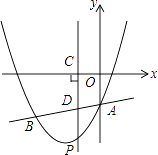
��1���������ߵĽ���ʽ��
��2����O��A��P��DΪ�����ƽ���ı����Ƿ���ڣ�����ڣ����P�����ꣻ�������ڣ�˵�����ɣ�
��3������P�˶���ֱ��AB�·�ijһ��ʱ������P��PM��AB������ΪM������PAʹ��PAMΪ����ֱ�������Σ���ֱ��д����ʱ��P�����꣮
���𰸡�
��1��
�⣺��ֱ��y= ![]() x��3����A��B���㣬���е�A��y���ϣ�
x��3����A��B���㣬���е�A��y���ϣ�
��A��0����3����
��B����4����5����
�� ![]() ��
��
�� 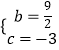 ��
��
�������߽���ʽΪy=x2+ ![]() x��3��
x��3��
��2��
�⣺���ڣ�
��P��m��m2+ ![]() m��3������m��0����
m��3������m��0����
��D��m�� ![]() m��3����
m��3����
��PD=|m2+4m|
��PD��AO��
�൱PD=OA=3���ʴ�����O��A��P��DΪ�����ƽ���ı��Σ�
��|m2+4m|=3��
�ٵ�m2+4m=3ʱ��
��m1=��2�� ![]() ��m2=��2+
��m2=��2+ ![]() ���ᣩ��
���ᣩ��
��m2+ ![]() m��3=��1��
m��3=��1�� ![]() ��
��
��P����2�� ![]() ����1��
����1�� ![]() ����
����
�ڵ�m2+4m=��3ʱ��
��m1=��1��m2=��3��
(i)m1=��1��
��m2+ ![]() m��3=��
m��3=�� ![]() ��
��
��P����1���� ![]() ����
����
(ii)m2=��3��
��m2+ ![]() m��3=��
m��3=�� ![]() ��
��
��P����3���� ![]() ����
����
���P����������2�� ![]() ����1��
����1�� ![]() ��������1����
��������1���� ![]() ��������3����
��������3���� ![]() ����
����
��3��
�⣺����һ����ͼ��
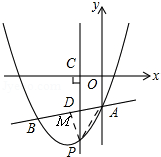
�ߡ�PAMΪ����ֱ�������Σ�
���BAP=45�㣬
��ֱ��AP���Կ�����ֱ��AB�Ƶ�A��ʱ����ת45�����ã�
��ֱ��AP����ʽΪy=kx��3��
��ֱ��AB����ʽΪy= ![]() x��3��
x��3��
��k= ![]() =3��
=3��
��ֱ��AP����ʽΪy=3x��3��
���� 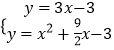 ��
��
��x1=0���ᣩx2=�� ![]()
��x=�� ![]() ʱ��y=��
ʱ��y=�� ![]() ��
��
��P���� ![]() ����
���� ![]() ����
����
����������ͼ��
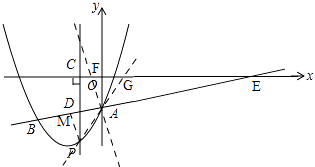
��ֱ��AB����ʽΪy= ![]() x��3��
x��3��
��ֱ��AB��x��Ľ�������ΪE��6��0����
����A��AF��AB��x���ڵ�F��
��A��0����3����
��ֱ��AF����ʽΪy=��2x��3��
��ֱ��AF��x��Ľ���ΪF���� ![]() ��0����
��0����
��AE=3 ![]() ��AF=
��AF= ![]() ��
��
����A����EAF�Ľ�ƽ���߽�x���ڵ�G��������������ڵ�P������P��PM��AB��
���EAG=45�㣬
���BAP=45�㣬
������PAMΪ����ֱ�������Σ�
���G��m��0����
��EG=6��m��FG=m+ ![]() ��
��
���ݽ�ƽ���߶����ã� ![]() ��
��
�� ![]() ��
��
��m=1��
��G��1��0����
��ֱ��AG����ʽΪy=3x��3�٣�
�������߽���ʽΪy=x2+ ![]() x��3�ڣ�
x��3�ڣ�
�����٢ڵã�x=0���ᣩ��x=�� ![]() ��
��
��y=�� ![]() ��
��
��P���� ![]() ����
���� ![]() ����
����
����������1����ȷ������A���꣬Ȼ���ô���ϵ�����������߽���ʽ����2����ȷ����PD=|m2+4m|����PD=OA=3���ʴ�����O��A��P��DΪ�����ƽ���ı��Σ��õ�|m2+4m|=3������������������ۼ��㼴�ɣ���3���ɡ�PAMΪ����ֱ�������Σ��õ���BAP=45�㣬�Ӷ����ֱ��AP�Ľ���ʽ��������ֱ��AP�������ߵĽ������꼴�ɣ�

����Ŀ��2013����һ�����˼������µ�����������������������ҹ��ֵ����������г�����������ij�콢������8000Ԫ�����ס��������ͺŵĿ��������������2800Ԫ�����ۺ��ۼ����±���
Ʒ�� �۸� | ���Ϳ��� | ���Ϳ��� |
������Ԫ/���� | 20 | 25 |
�ۼ���Ԫ/���� | 26 | 35 |
��1��������깺���ס��������ͺſ��ָ����ٴ���
��2��������ڶ�����ԭ�۹����ס��������ͺſ��������������ͺſ��ִ��������������������ͺſ��ִ����ǵ�һ�ε�2�������ֿ��ְ�ԭ�ۼ۳����������ֿ��������������������ͺŵĿ��ֶ�������Ҫʹ�ڶ������ۻ����������3680Ԫ�������ͺŵĿ�������ۼ�Ϊÿ������Ԫ��
����Ŀ����ͼ�����������������һ����������ת����ת�̣����涨���˿�����20Ԫ���Ͼ��ܻ��һ��ת��ת�̵Ļ��ᣬ��ת��ֹͣʱ��ָ��������һ����Ϳ��Ի����Ӧ�Ľ�Ʒ���±��ǻ�����е�һ��ͳ�����ݣ�
ת��ת�̵Ĵ���n | 100 | 200 | 400 | 500 | 1000 |
���ڡ����ࡱ����Ĵ���m | 32 | 58 | 121 | 149 | 300 |
���ڡ����ࡱ�����Ƶ�� | 0.3025 |
(1)���㲢�������ı���
(2)����ƣ���n�ܴ�ʱ��Ƶ�ʽ���ӽ����٣�
(3)������ȥת����ת��һ�Σ���������ĸ����Ƕ��٣�
����Ŀ���������Ϊ�Ӽס��������˶�Ա��ѡ��һ�˲μ�ʡ����,�����ǽ��������β���,���Գɼ����:
ѡ�� | ѡ�γɼ�/�� | ��λ�� | ƽ���� | |||||
�� | 10 | 9 | 8 | 8 | 10 | 9 | ||
�� | 10 | 10 | 8 | 10 | 7 | 9 | ||
(1)�ѱ������ո���������д����;
(2)�ֱ����ס������β��Գɼ��ķ���;
(3)����(1),(2)����Ľ��,����Ϊ�Ƽ�˭�μ�ʡ����������?��˵������.