题目内容
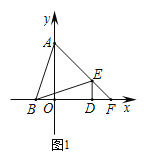
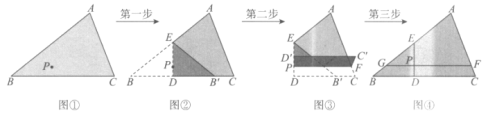
【题目】如图,正方形ABCD和正方形BEFG的边长分别为1和3,点C在边BG上,线段DF、EG交于点M,连接DE、BM,则△DEG的面积为____,BM=____.

【答案】![]()
![]() .
.
【解析】
依据五边形AEFGD的面积减去△ADE和△EFG的面积,即可得到△DEG的面积;连接BD,BF,即可得到△BDF是直角三角形,然后证明M是DF的中点,再根据勾股定理求出DF的长,依据直角三角形斜边上中线的性质即可得出BM的长.
根据题意得:△DEG的面积为:12+32![]() 1×(3﹣1)
1×(3﹣1)![]() 1×(1+3)
1×(1+3)![]() 32=1+9+1﹣2
32=1+9+1﹣2![]() ,
,
如图,连接BD,BF,则∠DBF=90°,
∴△BDF是直角三角形.
∵BM与FM关于GE对称,
∴BM=FM,
∴∠MBF=∠MFB,
又∵∠MBF+∠MBD=∠MFB+∠MDB,
∴∠MDB=∠MBD,
∴DM=BM,
∴M是DF的中点,
∴Rt△BDF中,BM![]() DF.
DF.
∵正方形ABCD和正方形BEFG的边长分别为1和3,
∴BD![]() ,BF=3
,BF=3![]() ,
,
∴DF![]() 2
2![]() ,
,
∴BM![]() .
.
故答案为:![]() ,
,![]() .
.


练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
【题目】我市2013年体育中考考试方案公布后,同学们将根据自己平的运动成绩确定自己的报考项目,下面是小亮同学近期在两个项目中连续五次测试的(得分情况得分统计表得分折线图)
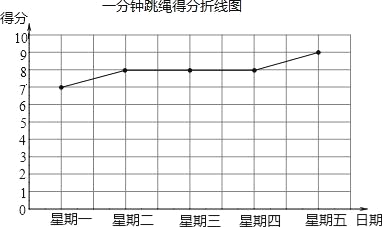
立定跳远测试日期 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
得分 | 7 | 10 | 8 | 9 | 6 |
(1)请根据图表信息,分别计算小亮这两个项目测试成绩的平均数和方差;
(2)根据以上信息,你认为在立定跳远和一分钟跳绳这两个项目中,小亮应选择哪个项目作为体育考试的报考项目?并简述理由.