题目内容
【题目】如图,在Rt△ABC中,∠BAC=90°,现在有一足够大的直角三角板,它的直角顶点D是BC上一点,另两条直角边分别交AB、AC于点E、F.
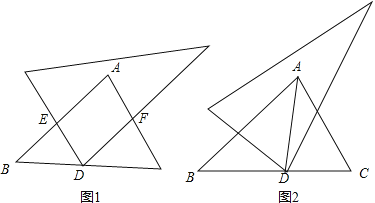
(1)如图1,若DE⊥AB,DF⊥AC,求证:四边形AEDF是矩形;
(2)在(1)条件下,若点D在∠BAC的 角平分线上,试判断此时四边形AEDF的形状,并说明理由;
(3)若点D在∠BAC的角平分线上,将直角三角板绕点D旋转一定的角度,使得直角三角板的两条边与两条直角边分别交于点E、F(如图2),试证明AE+AF=![]() AD.
AD.
【答案】见解析
【解析】解:(1)∵DE⊥AB,BF⊥AC,
∴∠AED=∠AFD=90°,
∵∠BAC=90°,
∴四边形AEDF是矩形;
(2)四边形AEDF是正方形,
理由:∵点D在∠BAC的 角平分线上,DE⊥AB,BF⊥AC,
∴DE=DF,
∴矩形AEDF是正方形;
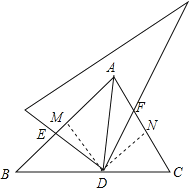
(3)作DM⊥AB于M,DN⊥AC于N,
∴∠AED=∠AFD=∠BAC=90°,
∵点D在∠BAC的 角平分线上,
∴DM=DN,
∴四边形AMDN是正方形,
∴AM=DM=DN=AN,∠MDN=∠AMD=90°,
∴∠MDF+∠NDF=90°,
∵∠EDF=90°,
∴∠MDF+∠EDM=90°,
∴∠NDF=∠EDM,
在△EMD与△END中, ,
,
∴△EMD≌△END,
∴EM=FN,
∵∠AMD=90°,
∴AM2+DM2=AD2,
∴AD=![]() AM,
AM,
∵AM=![]() (AM+AN)=
(AM+AN)=![]() (AE+AF),
(AE+AF),
∴AD=![]() ×
×![]() (AE+AF),
(AE+AF),
∴AE+AF=![]() AD.
AD.

练习册系列答案
相关题目