题目内容
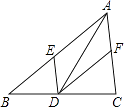
【题目】在△ABC中,点E、D、F分别在AB、BC、AC上且DE∥CA,DF∥BA,下列四个判断中不正确的是( ) 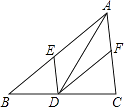
A.四边形AEDF是平行四边形
B.如果∠BAC=90°,那么四边形AEDF是矩形
C.如果AD⊥BC,那么四边形AEDF是菱形
D.如果AD平分∠BAC,那么四边形AEDF是菱形
【答案】C
【解析】解:由DE∥CA,DF∥BA,根据两组对边分别平行的四边形是平行四边形可得四边形AEDF是平行四边形;
又有∠BAC=90°,根据有一角是直角的平行四边形是矩形,可得四边形AEDF是矩形.故A、B正确;
如果AD平分∠BAC,那么∠EAD=∠FAD,又有DF∥BA,可得∠EAD=∠ADF,
∴∠FAD=∠ADF,
∴AF=FD,那么根据邻边相等的平行四边形是菱形,可得四边形AEDF是菱形,故D正确;
故选C.
【考点精析】解答此题的关键在于理解平行四边形的判定的相关知识,掌握两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形,以及对菱形的判定方法的理解,了解任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目