题目内容
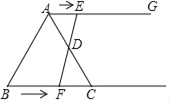
【题目】如图,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以lcm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s).
(1)连接EF,当EF经过AC边的中点D时,试判定四边形AFCE的形状并说明理由;
(2)当t为多少时,四边形ACFE是菱形.
【答案】(1)四边形AFCE是平行四边形.理由见解析;(2)t=6.
【解析】
(1)证△ADE≌△CDF(AAS),得DE=DF,从对角线角度证四边形AFCE是平行四边形;(2)根据菱形性质求解.
(1)解:四边形AFCE是平行四边形.
理由:∵AG∥BC,
∴∠EAD=∠DCF,∠AED=∠DFC,
∵D为AC的中点,
∴AD=CD,
在△ADE和△CDF中,
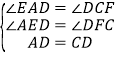 ,
,
∴△ADE≌△CDF(AAS),
∴DE=DF
∴四边形AFCE是平行四边形;
(2)解:若四边形ACFE是菱形,则有CF=AC=AE=6,
则此时的时间t=6÷1=6(s).

练习册系列答案
相关题目
【题目】“发展脐橙产业,加快脱贫的步伐”.某脐橙种植户新鮮采摘了20筐脐橙,以每筐25千克为标准重量,超过或不足干克数分别用正,负数来表示,记录如下:
与标准重量的差值(单位:干克) | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
筐数 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)与标准重量比较,20筐脐橙总计超过或不足多少千克?
(2)若脐橙毎干克售价6.5元,则出售这20筐脐橙可获得多少元?