Question

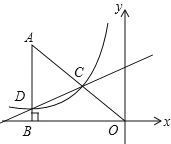
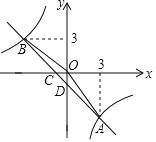
【题目】如图，已知直线与抛物线相交于，两点，抛物线交轴于点，交轴正半轴于点，抛物线的顶点为．

（1）求抛物线的解析式；

（2）设点为直线下方的抛物线上一动点，当的面积最大时，求的面积及点的坐标；

（3）若点为轴上一动点，点在抛物线上且位于其对称轴右侧，当与相似时，求点的坐标．

Answer 1

【答案】（1）y=；（2），；（3）或或或

【解析】

（1）将点代入中求出点B坐标，将点A，B，C坐标代入中求解即可；

（2）如图所示作辅助线，设点P，点E，表达出EP的长度，将△ABP分割成两个三角形进行计算，再利用二次函数的性质求最大值即可；

（3）通过坐标得出△MAD是等腰直角三角形，从而判断也是等腰直角三角形，再对进行分类讨论．

解：（1）将点代入中得，

∴点，

将点、、代入中得

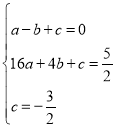，解得：，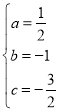

∴

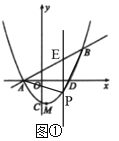
（2）如图①，过点P作EP⊥x轴，交AB于点E，则设点P，点E，

∴EP=，

∴

∵，开口向下，

∴当时，最大，

此时P

（3）在中，令y=0得，

解得，

∴点D（3，0）

又∵M（1，-2）

∴AD=4，AM=DM=，

∵

∴△MAD是等腰直角三角形，

若与相似，则也是等腰直角三角形，

有以下情况：

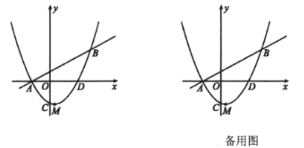
①当∠MQN=90°，且点N与点D重合时，如下图所示，满足要求，此时N（3，0）

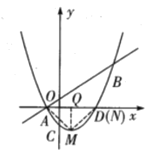
②当∠MQN=90°，点N在x轴上方时，如下图所示，作NF⊥x轴，ME⊥于x轴，

则△NFQ≌△QEM（AAS），

∴EM=FQ=2，EQ=NF

设 （ ），则

∴EQ=t+2-1=t+1

∴

解得：，（舍去），

∴N

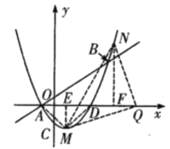
③当∠QMN=90°时， △与重合，N（3，0），

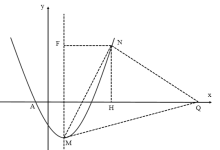
④当∠QNM=90°时，且点N在x轴上方时，如图所示作NH⊥x轴，NF⊥直线x=1

则△QHN≌△MFN，

∴FN=NH

设，则,

∴

解得：（舍去）

此时N

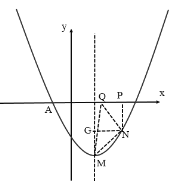
⑤当∠QNM=90°时，且点N在x轴下方时，如图所示作NP⊥x轴，NG⊥直线x=1，

则△QPN≌△NGM

∴PN=GN

设，则, ，

∴

解得（舍去）

此时N

综上所述，或或或．