题目内容
【题目】解不等式组 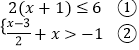 ;并写出解集中的整数解.
;并写出解集中的整数解.
【答案】解:解不等式组 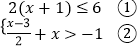 ;
;
解不等式①得:x≤2,
解不等式②得:x> ![]() ,
,
∴不等式组的解集为: ![]() <x≤2;
<x≤2;
∴整数解为:1,2.
【解析】一般先求出其中各不等式的解集,然后依据同大取大;同小取小;大小小大中间找;大大小小找不到确定出不等式组的解集,最后,再找出不等式组的整数解即可.
【考点精析】根据题目的已知条件,利用一元一次不等式组的解法和一元一次不等式组的整数解的相关知识可以得到问题的答案,需要掌握解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 );使不等式组中的每个不等式都成立的未知数的值叫不等式组的解,一个不等式组的所有的解组成的集合,叫这个不等式组的解集(简称不等式组的解).

练习册系列答案
相关题目
【题目】某少年宫管、弦乐队共46人.其中管乐队人数少于23人,弦乐队人数不足45人,现准备
购买演出服装.下面是某服装厂给出的演出服装的价格
购买服装的套数 | 1套至23套 | 24套至44套 | 45套及以上 |
每套服装的价格 | 60元 | 50元 | 40元 |
如果管乐队、弦乐队分别单独购买服装,一共需付2500元.
(1)管乐队、弦乐队各多少人?
(2)如果管乐队、弦乐队联合起来购买服装.那么比两队各自购买服装共可以节省多少钱?