题目内容
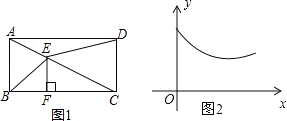
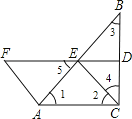
【题目】如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于D,交AB于E,点F在DE的延长线上,且AF=CE=AE.
(1)求证:四边形ACEF是平行四边形;
(2)当∠B=30°时,试猜想四边形ACEF是什么图形,并说明理由.
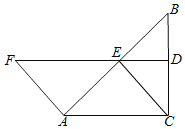
【答案】(1)见解析;(2)四边形ACEF为菱形,见解析.
【解析】
(1)易知DE是△ABC的中位线,则FE∥AC,BE=EA=CE=AF;因此△AFE、△AEC都是等腰三角形,可得∠F=∠5=∠1=∠2,即∠FAE=∠AEC,由此可证得AF∥EC,即可得出结论;
(2)证出AC=CE,即可得出结论.
(1)证明:∵DE垂直平分BC,
∴D为BC的中点,ED⊥BC,
又∵AC⊥BC,
∴ED∥AC,
∴E为AB中点,
∴ED是△ABC的中位线.
∴BE=AE,FD∥AC.
∴CE是是△ABC斜边上的中线
∴CE=![]() AB,
AB,
∵CE=AE=AF.
∴∠F=∠5=∠1=∠2.
∴∠FAE=∠AEC.
∴AF∥EC.
又∵AF=EC,
∴四边形ACEF是平行四边形;
(2)解:当∠B=30°时,四边形ACEF为菱形;
理由:∵∠ACB=90°,∠B=30°,
∴AC=![]() AB,
AB,
由(1)知CE=![]() AB,
AB,
∴AC=CE
又∵四边形ACEF为平行四边形
∴四边形ACEF为菱形.

练习册系列答案
相关题目