Question

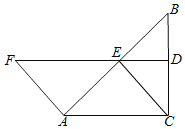
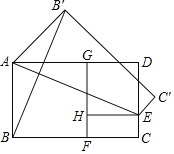
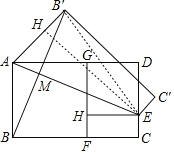
【题目】如图，在黄金矩形ABCD中，四边形ABFG、GHED均为正方形，，现将矩形ABCD沿AE向上翻折，得四边形AEC'B'，连接BB'，若AB＝2，则线段BB'的长度为（　　）

A.B.C.2D.

Answer 1

【答案】A

【解析】

BB′交AE于M，作EH⊥AB′于H，连接B′E，如图，利用黄金矩形的定义得到BC＝+1，再利用正方形的性质得到AG＝AB＝2，DE＝DG＝﹣1，则利用勾股定理得到AE＝2，接着利用折叠的性质得到C′B′＝CB＝+1，EC′＝EC＝3﹣，AB′＝AB＝2，BB′⊥AE，B′M＝BM，则EH＝C′B′＝+1，然后利用面积法求出B′M，从而得到BB′的长．

解：BB′交AE于M，作EH⊥AB′于H，连接B′E，如图，

∵四边形ABCD为黄金矩形，

∴AB＝BC，

∴BC＝×2＝+1，

∵四边形ABFG、GHED均为正方形，

∴AG＝AB＝2，DE＝DG＝+1﹣2＝﹣1，

在Rt△ADE中，AE＝＝2，

∵矩形ABCD沿AE向上翻折，得四边形AEC'B'，

∴C′B′＝CB＝+1，EC′＝EC＝3﹣，AB′＝AB＝2，BB′⊥AE，B′M＝BM，

易得四边形B′C′EH为矩形，则EH＝C′B′＝+1，

∵B′M×AE＝AB′×EH，

∴B′M＝＝，

∴BB′＝2B′M＝．

故选：A．