题目内容
【题目】如图,将边长为2的等边三角形ABC绕点C旋转120°,得到△DCE,连接BD,则BD的长为( ) 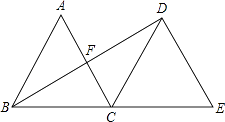
A.2
B.2.5
C.3
D.2 ![]()
【答案】D
【解析】解:连接AD,由题意知,△ABC≌△EDC,∠ACE=120°, 又∵△ABC是等边三角形,
∴AB=DC=BC=DE=5,∠ABC=∠ACB=∠DCE=∠E=60°,
∴∠ACE+∠ACB=120°+60°=180°,
∴B、C、E三点在一条直线上.
∴AB∥DC,
∴四边形ABCD为菱形,
∴∠DBE= ![]() ∠ABC=30°,
∠ABC=30°,
∵∠DBE+∠BDE+∠E=180°,
∴∠BDE=90°.
∵B、C、E三点在一条直线上,
∴BE=4,
∴BD= ![]() =
= ![]() =2
=2 ![]() .
.
故选:D.
【考点精析】通过灵活运用等边三角形的性质和旋转的性质,掌握等边三角形的三个角都相等并且每个角都是60°;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了即可以解答此题.

练习册系列答案
相关题目