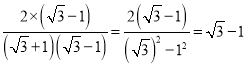题目内容
【题目】已知点A(-2,2),B(8,12)在抛物线y=ax2+bx上.
(1)求抛物线的解析式;
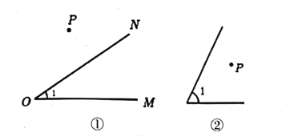
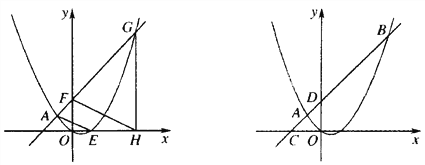
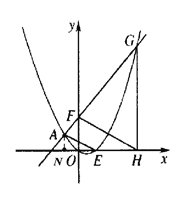
(2)如图1,点F的坐标为(0,m)(m>4),直线AF交抛物线于另一点G,过点G作x轴的垂线,垂足为H,设抛物线与x轴的正半轴交于点E,连接FH、AE,求![]() 之值(用含m的代数式表示);
之值(用含m的代数式表示);
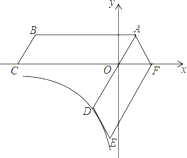
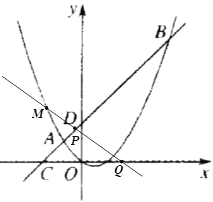
(3)如图2,直线AB分别交x轴、y轴于C、D两点,点P从点C出发,沿射线CD方向匀速运动,速度为每秒![]() 个单位长度,同时点Q从原点O出发,沿x轴正方向匀速运动,速度为每秒1个单位长度,点M是直线PQ与抛物线的一个交点,当运动到t秒时,QM=3PM,求t的值.
个单位长度,同时点Q从原点O出发,沿x轴正方向匀速运动,速度为每秒1个单位长度,点M是直线PQ与抛物线的一个交点,当运动到t秒时,QM=3PM,求t的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,
,![]() ,
,![]() ,
,![]()
【解析】分析:(1)、根据点A、B的坐标利用待定系数法,即可求出抛物线的解析式;(2)、根据点A、F的坐标利用待定系数法,可求出直线AF的解析式,联立直线AF和抛物线的解析式成方程组,通过解方程组可求出点G的坐标,过A作AN⊥x轴于点N得出点N的坐标,根据方程求出x的值得出答案;(3)、根据点A、B的坐标利用待定系数法,可求出直线AB的解析式,进而可找出点P、Q的坐标,分点M在线段PQ上以及点M在线段QP的延长线上两种情况考虑,借助相似三角形的性质可得出点M的坐标,再利用二次函数图象上点的坐标特征可得出关于t的一元二次方程,解之即可得出结论.
详解:解:(1)、点A(-2,2),B(8,12)在抛物线y=ax2+bx上,∴![]() ∴
∴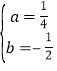 ,∴
,∴![]() ;
;
(2)、设直线AF的解析式为y=kx+m, ∵A(-2,2)在AF上,∴2=-2k+m,k=![]() (m-2),
(m-2),
∴直线y=kx+m可化为![]() , 则
, 则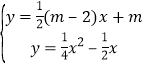
∴x2-2(m-1)x-4m=0, ∴(x+2)(x-2m)=0,∴x=-2或x=2m, ∴G的横坐标为2m,
∴OH=2m,∵OF=m,∴FH=![]() ,过A作AN⊥x轴于点N,则N(-2,0),
,过A作AN⊥x轴于点N,则N(-2,0),
令![]() ,∴x=0或x=2, ∴OE=2,NE=4 ∴AE=
,∴x=0或x=2, ∴OE=2,NE=4 ∴AE=![]() ,∴
,∴![]() ;
;
(3)、由题意A(-2,2),B(8,12),直线AB的解析式为:y=x+4,∠BCO=45°,
直线AB与x轴交点为C(-4,0),设P(t-4,t),则Q(t,0),设M(![]() ,
,![]() )
)
由QM=3PM可得,则|t-![]() |=3|
|=3|![]() -t+4|,
-t+4|,
(ⅰ)当t-![]() =3(
=3(![]() -t+4)即
-t+4)即![]() =t-3,直线PQ的解析式为tx+4y-t2=0,
=t-3,直线PQ的解析式为tx+4y-t2=0,
∴![]() =
=![]() ,∴M(t-3,
,∴M(t-3,![]() ),代入
),代入![]() 即
即![]() ,
,
∴t2-11t+15=0,∴![]() ,即:
,即:![]() ,
,![]() ;
;
(ⅱ)当![]() -t=3(
-t=3(![]() -t+4)即
-t+4)即![]() =t-6,∴
=t-6,∴![]() ,∴
,∴![]() ,
,
代入![]() 即
即![]() ,∴t2-20t+48=0,
,∴t2-20t+48=0,
∴![]() , 即:
, 即:![]() ,
,![]() ;
;
综上所述,所求t为:![]() ,
,![]() ,
,![]() ,
,![]() .
.

 阅读快车系列答案
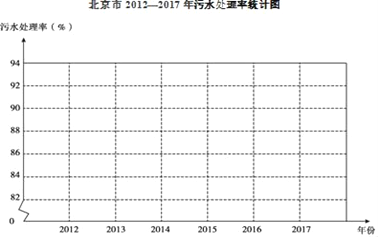
阅读快车系列答案【题目】北京市积极开展城市环境建设,其中污水治理是重点工作之一,以下是北京市2012﹣2017年污水处理率统计表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
污水处理率(%) | 83.0 | 84.6 | 86.1 | 87.9 | 90.0 | 92.0 |
(1)用折线图将2012﹣2017年北京市污水处理率表示出来,并在图中标明相应的数据;
(2)根据统计图表中提供的信息,预估2018年北京市污水处理率约为_____%,说明你的预估理由:_____.