题目内容
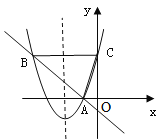
【题目】已知:抛物线y=x2+4x+4+m的图像与y轴交于点C,点B与点C的纵坐标相同,一次函数y=kx+b的与二次函数交于A、B两点,且A点坐标为(-1,0).
(1)求二次函数与一次函数的解析式;
(2)若抛物线对称轴上存在一点P,直线PC将△ABC分成面积为1:2两部分,求P点坐标。
【答案】(1)二次函数的解析式为y=x2+4x+3 ,一次函数的解析式为:y=-x-1;(2) P1(-2,1 ),P2(-2, ![]() ).
).
【解析】解:(1)因为A(-1,0)在抛物线y=x2+4x+4+m上
![]() =-1
=-1
所以二次函数的解析式为y=x2+4x+3
所以B点的坐标为(-4,3)
设BA的解析式为y=kx+b过A(-1,0),B (-4,-3)点
![]() 得 -k+b=0
得 -k+b=0
-4k+b=3
得k=-1 b=-1
BA的解析式为:y=-x-1
(2) P1(-2,1 ) P2(-2, ![]() )
)

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
