题目内容
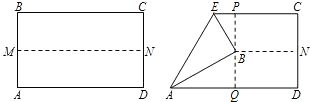
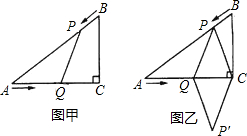
已知：如图，点E为四边形ABCD外一点，连接EB、EA、ED、EC，其中EA、ED与BC交点分别为M、N，且AD∥BC，AE=DE，BE=CE．求证：AB=DC．分析：根据外角的性质可得出∠AMB=∠BEM+∠EBM，∠DNC=∠CEN+∠ECN，再由BE=CE，得∠EBM=∠ECN，从而得出∠AEB=∠DEC，则△ABE≌△DEC，则AB=CD．
解答：证明：∵BE=CE，
∴∠EBM=∠ECN，
∵∠AMB=∠BEM+∠EBM，∠DNC=∠CEN+∠ECN，
∴∠AEB=∠DEC，
在△ABE和△DEC中，
，
∴△ABE≌△DEC（SAS），
∴AB=CD．
∴∠EBM=∠ECN，
∵∠AMB=∠BEM+∠EBM，∠DNC=∠CEN+∠ECN，
∴∠AEB=∠DEC，
在△ABE和△DEC中，
|
∴△ABE≌△DEC（SAS），
∴AB=CD．
点评：本题考查了全等三角形的判定和性质以及平行线的性质，是基础知识要熟练掌握．
练习册系列答案
相关题目
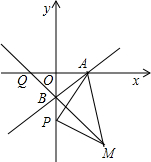B点下方一点，PB=m（m＞0），以AP为边作等腰直角三角形APM，其中PM=PA，点M落在第四象限．
、
、
、
分别是正方形ABCD四条边上的点，且△A
≌△B
≌△C
≌△D
．
为正方形．