题目内容
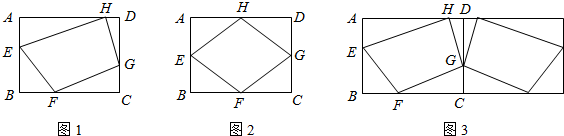
(2012•西城区一模)已知:如图1,矩形ABCD中,AB=6,BC=8,E、F、G、H分别是AB、BC、CD、DA四条边上的点(且不与各边顶点重合),设m=EF+FG+GH+HE,探索m的取值范围.
(1)如图2,当E、F、G、H分别是AB、BC、CD、DA四边中点时,m=
(2)为了解决这个问题,小贝同学采用轴对称的方法,如图3,将整个图形以CD为对称轴翻折,接着再连续翻折两次,
从而找到解决问题的途径,求得m的取值范围.①请在图3中补全小贝同学翻折后的图形;②m的取值范围是
(1)如图2,当E、F、G、H分别是AB、BC、CD、DA四边中点时,m=
20
20
.(2)为了解决这个问题,小贝同学采用轴对称的方法,如图3,将整个图形以CD为对称轴翻折,接着再连续翻折两次,
从而找到解决问题的途径,求得m的取值范围.①请在图3中补全小贝同学翻折后的图形;②m的取值范围是
20≤m<28
20≤m<28
.
分析:(1)利用勾股定理求出矩形对角线的长度,再利用三角形中位线的性质得出EH=
BD,EF=
AC,FG=
BD,HG=
AC,进而求出即可;
(2)①利用轴对称图形的性质得出答案即可;
②利用两点之间线段最短以及三角形三边关系得出m的取值范围即可.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)①利用轴对称图形的性质得出答案即可;
②利用两点之间线段最短以及三角形三边关系得出m的取值范围即可.
解答: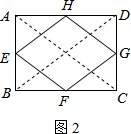 解:(1)如图2,连接AC,BD,
解:(1)如图2,连接AC,BD,
∵在矩形ABCD中,AB=6,BC=8,
∴AC=BD=
=10,
∵E、F、G、H分别是AB、BC、CD、DA四边中点,
∴EH,EF,FG,HG,分别是△ABD,△ABC,△BCD,△ACD的中位线,
∴EH=
BD,EF=
AC,FG=
BD,HG=
AC,
∴m=EF+FG+GH+HE=AC+BD=10+10=20;
(2)①如图3所示(虚线可以不画),
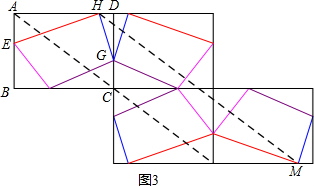
②由图形可知,四边形的周长即折线HM的长,由两点之间线段最短可知,折线HM≥20,即周长不小于20;
又由题可知,四边形周长小于矩形ABCD的周长,即周长小于28,
故20≤m<28.
故答案为:20;20≤m<28.
 解:(1)如图2,连接AC,BD,
解:(1)如图2,连接AC,BD,∵在矩形ABCD中,AB=6,BC=8,
∴AC=BD=
| 62+82 |
∵E、F、G、H分别是AB、BC、CD、DA四边中点,
∴EH,EF,FG,HG,分别是△ABD,△ABC,△BCD,△ACD的中位线,
∴EH=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴m=EF+FG+GH+HE=AC+BD=10+10=20;
(2)①如图3所示(虚线可以不画),

②由图形可知,四边形的周长即折线HM的长,由两点之间线段最短可知,折线HM≥20,即周长不小于20;
又由题可知,四边形周长小于矩形ABCD的周长,即周长小于28,
故20≤m<28.
故答案为:20;20≤m<28.
点评:此题主要考查了翻折变换的性质以及矩形的性质和三角形中位线的性质等知识,利用翻折变换的性质得出折线HM与四边形的周长关系是解题关键.

练习册系列答案
相关题目
