Question

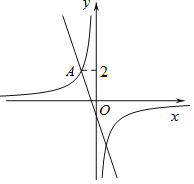
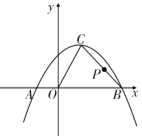
【题目】已知：如图，抛物线与轴交于点．

(1)试确定该抛物线的函数表达式；

(2)已知点是该抛物线的顶点，求的面积；

(3)若点是线段上的一动点，求的最小值．

Answer 1

【答案】（1）；（2）；（3）OP的最小值是．

【解析】

（1）将点A与点B坐标代入抛物线解析式得到关于的方程组，由此求出的值，从而进一步得出解析式即可；

（2）利用配方法求出抛物线的顶点坐标，然后根据三角形的面积公式进一步计算即可；

（2）根据垂线段最短可知当OP⊥BC时，OP最小，据此进一步利用三角形的面积公式求出OP即可.

（1）∵抛物线与轴交于点A(，0)与点B(3，0)，

∴

解得：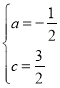

∴抛物线的解析式为；

（2）∵，

∴抛物线的顶点的坐标为(1，2)．

∴；

（3）当是边上的高时，的值最小，

∵B点坐标为(3，0)，C点坐标为(1，2)，

∴

∵，

∴，

即OP的最小值是．