题目内容
含60°角的菱形A1B1C1B2,A2B2 C2B3,A3B3C3B4,…,按如图的方式放置在平面直角坐标系xOy中,点A1,A2,A3,…,和点B1,B2,B3,B4,…,分别在直线y=kx和x轴上.已知B1(2,0),B2(4,0),则点A1的坐标是 ;点A3的坐标是 ;点An的坐标是 (n为正整数).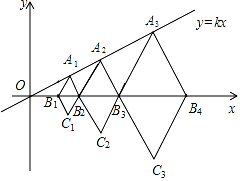
(3,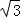 ),(9,3
),(9,3 ),(3n,
),(3n, n).
n).
解析试题分析:利用菱形的性质得出△A1B1B2是等边三角形,进而得出A1坐标,进而得出OB2=A2B2=4,即可得出A3,An的坐标.
过点A1作A1D⊥x轴于点D,
∵含60°角的菱形A1B1C1B2,A2B2 C2B3,A3B3C3B4,…,
∴∠A1B1D=60°,A1B1=A1B2,
∴△A1B1B2是等边三角形,
∵B1(2,0),B2(4,0),
∴A1B1=B1B2=2,
∴B1D=1,A1D=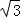 ,∴OD=3,
,∴OD=3,
则A1(3,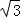 ),
),
∴tan∠A1OD= ,
,
∴∠A1OD=30°,
∴OB2=A2B2=4,
同理可得出:A2(6,2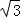 ),则A3(9,3
),则A3(9,3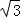 ),
),
则点An的坐标是:(3n,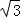 n).
n).
故答案为:(3,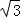 ),(9,3
),(9,3 ),(3n,
),(3n, n).
n).
考点:1.菱形的性质;2.一次函数图象上点的坐标特征.

练习册系列答案
相关题目
若点(-4,y1),(2,y2)都在直线y=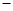 3x+t上,则y1与y2的大小关系是 ( )
3x+t上,则y1与y2的大小关系是 ( )
| A.y1>y2 | B.y1=y2 | C.y1<y2 | D.无法确定 |
若反比例函数 的图象过点(﹣2,1),则一次函数y=kx﹣k的图象过
的图象过点(﹣2,1),则一次函数y=kx﹣k的图象过
| A.第一、二、四象限 | B.第一、三、四象限 |
| C.第二、三、四象限 | D.第一、二、三象限 |
 图像向下平移
图像向下平移 个单位,与双曲线
个单位,与双曲线 交于点A,与
交于点A,与 轴交于点B,则
轴交于点B,则 =( )
=( )




 平移后经过点(2,
平移后经过点(2, ),则平移后的直线解析式为______________.
),则平移后的直线解析式为______________.