题目内容
已知在平面直角坐标系中,点O为坐标原点,过O的直线OM经过点A(6,6),过A作正方形ABCD,在直线OA上有一点E,过E作正方形EFGH,已知直线OC经过点G,且正方形ABCD的边长为2,正方形EFGH的边长为3,则点F的坐标为 .
(9,6).
解析试题分析:先利用待定系数法确定直线OA的解析式为y=x,根据坐标与图形变换由点A(6,6),正方形ABCD的边长为2得到D点坐标为(8,6),C点坐标为(8,4),再利用待定系数法确定直线OC的解析式为y= x,则可设G点坐标为(t,
x,则可设G点坐标为(t, t),由于正方形EFGH的边长为3,所以H点坐标为(t,
t),由于正方形EFGH的边长为3,所以H点坐标为(t, t+3),从而得到E点坐标为(t-3,
t+3),从而得到E点坐标为(t-3, t+3),然后把把E点坐标代入y=x求出t=12,得到E点坐标为(9,9),再把E点向下平移3个单位即可得到F点的坐标.
t+3),然后把把E点坐标代入y=x求出t=12,得到E点坐标为(9,9),再把E点向下平移3个单位即可得到F点的坐标.
试题解析:设直线OA的解析式为y=mx,
把A(6,6)代入得6m=6,解得m=1,
∴直线OA的解析式为y=x,
∵点A(6,6),正方形ABCD的边长为2,
∴D点坐标为(8,6),C点坐标为(8,4).
设直线OC的解析式为y=kx,
把C(8,4)代入y=kx
得8k=4,解得k= ,
,
∴直线OC的解析式为y= x,
x,
设G点坐标为(t, t),
t),
∵正方形EFGH的边长为3,
∴H点坐标为(t, t+3),E点坐标为(t-3,
t+3),E点坐标为(t-3, t+3),
t+3),
把E(t-3, t+3)代入y=x
t+3)代入y=x
得t-3= t+3,解得t=12,
t+3,解得t=12,
∴E点坐标为(9,9),
∴F点的坐标为(9,6).
考点:1.一次函数图象上点的坐标特征;2.正方形的性质.

直线 经过点A(-1,
经过点A(-1, )与点B(
)与点B( ,1),其中
,1),其中 >1,则直线
>1,则直线 不经过( )
不经过( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
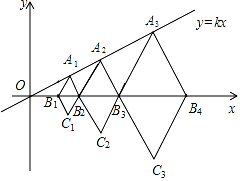
如图,在平面直角坐标系中,直线l:y= x+1交x轴于点A,交y轴于点B,点A1、A2、A3,…在x轴上,点B1、B2、B3,…在直线l上。若△OB1A1,△A1B2A2,△A2B3A3,…均为等边三角形,则△A5B6A6的周长是
x+1交x轴于点A,交y轴于点B,点A1、A2、A3,…在x轴上,点B1、B2、B3,…在直线l上。若△OB1A1,△A1B2A2,△A2B3A3,…均为等边三角形,则△A5B6A6的周长是
A.24 | B.48 | C.96 | D.192 |
直线y=kx+b不经过第四象限,则( )
| A.k>0,b>0 | B.k<0,b>0 | C.k≥0,b≥0 | D.k<0,b≥0 |