题目内容
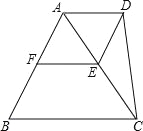
【题目】如图,点E、F分别是等边△ABC中AC、AB边上的中点,以AE为边向外作等边△ADE.
(1)求证:四边形AFED是菱形;
(2)连接DC,若BC=10,求四边形ABCD的面积.
【答案】(1)证明详见解析;(2)![]() .
.
【解析】
试题分析:(1)由等边三角形的性质得出AF=EF=AE=DE=AD,由四边相等的四边形是菱形,即可得出结论;
(2)作AM⊥BC于M,由等边三角形的性质和三角函数求出AM,在求出AD的长,证出四边形ABCD是梯形,由梯形的面积公式即可得出结果.
试题解析:(1)∵△ABC、△ADE是等边三角形,
∴AF=EF=AE=DE=AD,∠ACB=∠DAE=60°,
∴四边形AFED是菱形;
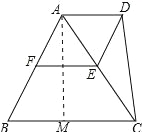
(2)解:作AM⊥BC于M,如图所示:
∵△ABC是等边三角形,
∴AC=BC=10,∠B=60°,
∴AM=ABsin60°=10×![]() =
=![]() ,
,
∵E是AC的中点,
∴AE=AD=![]() AC=5,
AC=5,
∵∠ACB=∠DAE=60°,
∴AD∥BC,
∴四边形ABCD是梯形,
∴四边形ABCD的面积=![]() (AD+BC)×AM=
(AD+BC)×AM=![]() (5+10)×
(5+10)×![]() =
=![]() .
.

练习册系列答案
相关题目

