题目内容
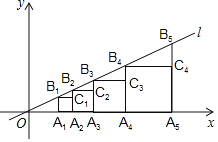
【题目】如图，已知直线l：y＝
x，点A1（2，0），过点A1作x轴的垂线交直线l于点B1，以A1B1为边，向右侧作正方形A1B1C1A2，延长A2C1交直线l于点B2；以A2B2为边，向右侧作正方形A2B2C2A3，延长A3C2交直线l于点B3；以A3B3为边，向右侧作正方形A3B3C3A4，延长A4C3交直线l于点B4；…；按照这个规律继续作下去，点Bn的横坐标为_．（结果用含正整数n的代数式表示）
【答案】
．
【解析】
先分别求出A1、B1的坐标，然后根据正方形的性质即可求出A2、B2的坐标，同理求出A3、B3的坐标，A4、B4的坐标，找出两点坐标变化规律，总结公式即可得出结论．
解：∵A1（2，0），将x=2代入y＝
x中，解得y=1
∴B1（2，1）=（
，
），
∴A1 B1=1
由正方形的性质，可求A2（3，0），
原理同上即可求出B2（3，
）=（
，
），
∴A2 B2=
由正方形的性质，可A3（
，0），
原理同上即可求出B3（，
）=（
，
），
同理可知：A4（
，0），B4（，
）=（
，
），
……
所以An（，0），Bn（，
），
∴点Bn的横坐标为，
故答案为．
练习册系列答案
尖子生新课堂课时作业系列答案
英才计划同步课时高效训练系列答案
相关题目
