题目内容
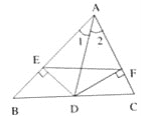
【题目】已知,如图,AD是△ABC的角平分线,DE、DF分别是△ABD和△ACD的高。求证:AD垂直平分EF。
【答案】见解析
【解析】
由DE⊥AB,DF⊥AC,得出∠AED=∠AFD;因为AD是△ABC的角平分线,可得∠1=∠2,DE=DF,推出△AED≌△AFD,即AE=AF,所以点A在EF的垂直平分线上,又DE=DF,推出点D在EF的垂直平分线上,即可证明AD垂直平分EF;
证明:∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD,
又∵AD是△ABC的角平分线,
∴∠1=∠2,DE=DF,
∴△AED≌△AFD(AAS),
∴AE=AF,
∴点A在EF的垂直平分线上(到线段两端距离相等的点在线段的垂直平分线上),
∵DE=DF,
∴点D在EF的垂直平分线上,
∴AD垂直平分EF.

练习册系列答案
相关题目