题目内容
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,F是DE延长线上的点,且EF=DE.
(1)图中的平行四边形有哪几个?请说明理由;
(2)若△AEF的面积是3,求四边形BCFD的面积.
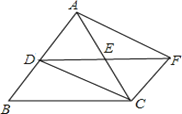
【答案】(1)图中的平行四边形有:平行四边形ADCF,平行四边形BDFC,理由见解析;
(2)平行四边形BCFD的面积为12.
【解析】试题分析:(1)由E为AC的中点,可得AE=CE,再由条件EF=DE可得四边形ADCF是平行四边形;(2)根据等底等高的三角形面积相等可得平行四边形对角线分成的四个小三角形面积相等可得△CEF的面积和△CED的面积都等于△AEF的面积为3,从而可得四边形BCFD的面积为12.
试题解析:(1)图中的平行四边形有:平行四边形ADCF,平行四边形BDFC,
理由是:∵E为AC的中点,
∴AE=CE,
∵DE=EF,
∴四边形ADCF是平行四边形,
∴AD∥CF,AD=CF,
∵D为AB的中点,
∴AD=BD,
∴BD=CF,BD∥CF,
∴四边形BDFC是平行四边形.
(2)由(1)知四边形ADCF是平行四边形,四边形BDFC是平行四边形,
∴S△CEF=S△CED=S△AEF=3,
∴平行四边形BCFD的面积是12.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目