题目内容
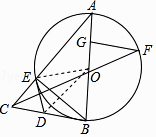
【题目】如图,△ABE是⊙O的内接三角形,AB为直径,过点B的切线与AE的延长线交于点C,D是BC的中点,连接DE,连接CO,线段CO的延长线交⊙O于F,FG⊥AB于G. 
(1)求证:DE是⊙O的切线;
(2)若AE=4,BE=2,求AG的长.
【答案】
(1)证明:连接OE,OD,
在△OED与△OBD中, 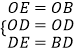 ,
,
∴△OED≌△OBD,
∴∠OED=∠OBD,
∵BC是⊙O的切线,
∴∠OBD=90°,
∴∠OED=90°,
∴OE⊥ED,
∴DE是⊙O的切线;
(2)解:∵AB为⊙O的直径,
∴∠AEB=90°,
∴AB= ![]() =2
=2 ![]() ,
,
∴OF=OB= ![]() ,
,
∵△AEB∽△BEC,
∴ ![]() ,
,
∴BC= ![]() =
= ![]() ,
,
∴OC= ![]() =
= ![]() =
= ![]() ,
,
∵∠AOF=∠BOC,
∵FG⊥AB,
∴∠FGO=90°,
∴∠FGO=∠OBC=90°,
∴△OFG∽△OBC,
∴ ![]() ,
,
∴OG= ![]() OB=
OB= ![]() ,
,
∴AG=AO﹣OG= ![]() ﹣
﹣ ![]() .
.
【解析】(1)连接OE,OD,根据全等三角形的性质得到∠OED=∠OBD,由BC是⊙O的切线,得到∠OBD=90°,于是得到结论;(2)由AB为⊙O的直径,得到∠AEB=90°,根据勾股定理得到AB= ![]() =2
=2 ![]() ,求得OF=OB=
,求得OF=OB= ![]() 根据相似三角形的性质得到BC=
根据相似三角形的性质得到BC= ![]() =
= ![]() ,根据勾股定理到OC=
,根据勾股定理到OC= ![]() =
= ![]() =
= ![]() ,根据相似三角形的性质即可得到结论.
,根据相似三角形的性质即可得到结论.

【题目】阅读以下材料,并按要求完成相应的任务.
几何中,平行四边形、矩形、菱形、正方形和等腰梯形都是特殊的四边形,大家对于它们的性质都非常熟悉,生活中还有一种特殊的四边形﹣﹣筝形.所谓筝形,它的形状与我们生活中风筝的骨架相似. |
|
如果只研究一般的筝形(不包括菱形),请根据以上材料完成下列任务:
如果只研究一般的筝形(不包括菱形),请根据以上材料完成下列任务:
(1)请说出筝形和菱形的相同点和不同点各两条;
(2)请仿照图1的画法,在图2所示的8×8网格中重新设计一个由四个全等的筝形和四个全等的菱形组成的新图案,具体要求如下:
①顶点都在格点上;
②所设计的图案既是轴对称图形又是中心对称图形;
③将新图案中的四个筝形都图上阴影(建议用一系列平行斜线表示阴影).







