题目内容
【题目】在△ABC中,AB=AC,D是线段BC的延长线上一点,以AD为一边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.
(1)如图,点D在线段BC的延长线上移动,若∠BAC=40![]() ,则∠DCE=
,则∠DCE= ![]() .
.
(2)设∠BAC=m,∠DCE=n.
①如图,当点D在线段BC的延长线上移动时,m与n之间有什么数量关系?请说明理由.
②当点D在直线BC上(不与B、C重合)移动时,m与n之间有什么数量关系?请直接写出你的结论.

【答案】(1)40;(2)①m=n,理由见解析;②m+n=180°
【解析】试题分析:(1)可证△ABD≌△ACE,可得∠ACE=∠B,即可解题;
(2)①根据△ABD≌△ACE可分别求得∠BCE用m和用n分别表示,即可求得m、n的关系;②分两种情况分析,第1种,当D在线段BC的延长线上或反向延长线上时,第2种,当D在线段BC上时.
试题解析:(1)∵∠DAE=∠BAC,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
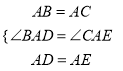 ,
,
∴△ABD≌△ACE(SAS),
∴∠ACE=∠B,
∵AB=AC,∠BAC=40°,
∴∠ACE=∠B=70°,
∴∠DCE=180°70°70°=40°;
(2) ①∵△ABD≌△ACE(1)已证,
∴∠ACE=∠B,
∵AB=AC,∠BAC=m,
∴∠ACE=∠B=∠ACB=![]() ,
,
∴∠BCE=∠ACB+∠ACE=180°m,
∵∠BCE=180°∠DCE=180°n,
∴m=n.
②当D在线段BC的延长线上或反向延长线上时,m=n,
当D在线段BC上时,m+n=180°.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目